The PyMC3 workflow¶
PyMC3 aims for intuitive and readable, yet powerful syntax that reflects how statisticians describe models. The modeling process generally follows these five steps:
- Encode a probability model by defining the following:
- The prior distributions that quantify knowledge and uncertainty about latent variables
- The likelihood function that conditions the parameters on observed data
- Analyze the posterior using one of the options:
- Obtain a point estimate using MAP inference
- Sample from the posterior using MCMC methods
- Approximate the posterior using variational Bayes.
- Check the model using various diagnostic tools.
- Generate predictions.
The resulting model can be used for inference to gain detailed insights into parameter values as well as to predict outcomes for new data points.
Logistic regression with PyMC3¶
Logistic regression estimates a linear relationship between a set of features and a binary outcome, mediated by a sigmoid function to ensure the model produces probabilities. The frequentist approach resulted in point estimates for the parameters that measure the influence of each feature on the probability that a data point belongs to the positive class, with confidence intervals based on assumptions about the parameter distribution.
In contrast, Bayesian logistic regression estimates the posterior distribution over the parameters itself. The posterior allows for more robust estimates of what is called a Bayesian credible interval for each parameter with the benefit of more transparency about the model’s uncertainty.
Imports¶
import warnings
warnings.filterwarnings('ignore')
from pathlib import Path
import pickle
from collections import OrderedDict
import pandas as pd
import numpy as np
from scipy import stats
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import (roc_curve, roc_auc_score, confusion_matrix, accuracy_score, f1_score,
precision_recall_curve)
import theano
import pymc3 as pm
from pymc3.variational.callbacks import CheckParametersConvergence
import statsmodels.formula.api as smf
import arviz as az
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.lines as mlines
import seaborn as sns
from IPython.display import HTML
sns.set(style="white", color_codes=True)
pd.set_option('display.max_columns', None)
data_path = Path('data')
fig_path = Path('figures')
model_path = Path('models')
for p in [data_path, fig_path, model_path]:
if not p.exists():
p.mkdir()
The Data¶
The goal of this dataset is to create a binary classification model that predicts whether or not over $11,000$ customers will subscribe to a term deposit after a marketing campaign the bank has performed, based on $17$ predictor variables. The target variable is given as deposit and takes on a value of $1$ if the customer has subscribed and $0$ otherwise.
This is a slightly imbalanced class problem because there are more customers that did not subscribe the term deposit than did.
Load from Disk¶
data = pd.read_csv('bank.csv')
data.info()
data.head()
unique = data.nunique()
unique
mask = data.nunique().values < 31
cat_features = list(unique[mask].index)
cat_features
Quick EDA¶
total = len(data)
plt.figure(figsize=(7,5))
g = sns.countplot(x='deposit', data=data)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
height = p.get_height()
g.text(p.get_x()+p.get_width()/2.,
height + 1.5,
'{:1.2f}%'.format(height/total*100),
ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()
fig, axs = plt.subplots(ncols=2, nrows=0, figsize=(13, 45))
plt.subplots_adjust(right=2)
plt.subplots_adjust(top=2)
for i, feature in enumerate(list(data[cat_features]), 1):
if(feature=='deposit'):
break
plt.subplot(len(cat_features), 3, i)
sns.countplot(y=feature, hue='deposit', data=data)
plt.title(f'{feature}', size=15, fontsize=12)
plt.legend(loc='best', prop={'size': 8})
plt.tight_layout()
plt.show()
plt.figure(figsize=(8,4))
sns.countplot(x='day', hue='deposit', data=data);
num_features = [f for f in data.columns if f not in cat_features]
num_features.remove('day')
num_features
basetable0 = pd.DataFrame(index=data.index)
basetable0['deposit'] = data['deposit']
deposit_dict = {'no': 0, 'yes': 1}
basetable0 = basetable0.replace({'deposit': deposit_dict})
for variable in num_features:
if len(data.groupby(variable)) > 31:
new_variable = "disc_" + variable
basetable0[new_variable] = pd.qcut(data[variable], 5, duplicates='drop')
basetable0.head()
def create_pig_table(basetable, target, variable):
groups = basetable[[target,variable]].groupby(variable)
pig_table = groups[target].agg(Incidence = np.mean, Size = np.size).reset_index()
return pig_table
def plot_pig(pig_table, variable):
plt.figure(figsize=(10, 4))
plt.ylabel("Size", rotation=0, rotation_mode="anchor", ha="right")
pig_table["Size"].plot(kind="bar", width=0.5, color="lightgray", edgecolor="none")
pig_table["Incidence"].plot(secondary_y=True)
plt.xticks(np.arange(len(pig_table)), pig_table[variable])
plt.xlim([-0.5, len(pig_table) - 0.5])
plt.ylabel("Incidence", rotation=0, rotation_mode="anchor", ha="left")
plt.title(f'{variable}')
plt.show()
variables = list(basetable0.drop('deposit', axis=1).columns)
pig_tables = {}
for variable in variables:
pig_table = create_pig_table(basetable0, 'deposit', variable)
pig_tables[variable] = pig_table
for variable in variables:
pig_table = create_pig_table(basetable0, "deposit", variable)
plot_pig(pig_table, variable)
Data Preprocessing¶
job_dict = {'management': 12, 'admin.': 11, 'entrepreneur': 10, 'technician': 9, 'services': 8, 'self-employed': 7,
'blue-collar': 6, 'retired': 5, 'housemaid': 4, 'unemployed': 3, 'unknown': 2, 'student': 1}
data = data.replace({'job': job_dict})
marital_dict = {'married': 4, 'single': 3, 'divorced': 2, 'unknown': 1}
data = data.replace({'marital': marital_dict})
data['marital'] = data['marital'].astype(int)
edu_dict = {'tertiary': 4, 'secondary': 3, 'primary': 2, 'unknown': 1}
data = data.replace({'education': edu_dict})
default_dict = {'no': 1, 'yes': 0}
data = data.replace({'default': default_dict})
housing_dict = {'no': 1, 'yes': 0}
data = data.replace({'housing': housing_dict})
loan_dict = {'no': 1, 'yes': 0}
data = data.replace({'loan': loan_dict})
contact_dict = {'cellular': 3, 'telephone': 2, 'unknown': 1}
data = data.replace({'contact': contact_dict})
poutcome_dict = {'success': 4, 'other': 3, 'unknown': 2, 'failure': 1}
data = data.replace({'poutcome': poutcome_dict})
month_dict = {'jan': 1, 'feb': 2, 'aug': 8, 'nov': 11, 'jun': 6, 'apr': 4, 'jul': 7, 'may': 5, 'oct': 10,
'mar': 3, 'sep': 9, 'dec': 12}
data = data.replace({'month': month_dict})
pdays_dict = {-1: 0}
data = data.replace({'pdays': pdays_dict})
data.head()
data.dtypes
mask = data.nunique().values > 31
num_features = list(unique[mask].index)
num_features
Distributions and transformations¶
data[num_features].hist(bins=30, figsize=(8,7))
plt.tight_layout();
from sklearn.preprocessing import MinMaxScaler
import scipy.stats as stats
colors = cm.rainbow(np.linspace(0, 1, len(num_features)))
for col, c in zip(num_features, colors):
minmax = MinMaxScaler(feature_range=(0.0001, max(data[col].values)))
if data[col].describe().iloc[3] <= 0.0:
z = minmax.fit_transform(data[col].values.reshape(-1, 1))
z = np.squeeze(z)
print('BC MinMax Scaled')
else:
z = data[col]
z0, _ = stats.boxcox(z, lmbda=None)
z1 = stats.boxcox(z, lmbda=-1)
z2 = stats.boxcox(z, lmbda=-0.5)
z3 = stats.boxcox(z, lmbda=0.0)
z4 = stats.boxcox(z, lmbda=0.5)
z5 = stats.boxcox(z, lmbda=2)
z6 = stats.boxcox(z, lmbda=-2)
z7 = np.cbrt(data[col])
trans = [data[col], z0, z1, z2, z3, z4, z5, z6, z7]
names = ['Original', 'Boxcox', 'Recip', 'Recip_Sqrt', 'Log', 'Sqrt', 'Square', 'Recip_Square', 'Cube_rt']
fig = plt.figure(figsize=(12,6))
for i, t, n in zip(range(1, 10), trans, names):
ax = fig.add_subplot(3, 3, i)
plt.hist(t, bins=30, color=c, alpha=0.6)
plt.title(col+'_'+n)
plt.tight_layout()
plt.show();
data.balance = np.cbrt(data.balance)
age, _ = stats.boxcox(data.age, lmbda=None)
data.age = age
duration, _ = stats.boxcox(data.duration, lmbda=None)
data.duration = duration
from sklearn.preprocessing import scale
cols = ['duration', 'balance', 'age']
data.loc[:, cols] = scale(data.loc[:, cols])
nums = data[num_features]
nums['deposit'] = data.deposit
sns.pairplot(nums, hue='deposit', diag_kind='hist');
deposit_dict = {'no': 0, 'yes': 1}
data = data.replace({'deposit': deposit_dict})
data.head()
Correlations¶
plt.figure(figsize=(13, 13))
corr = data.corr()
mask = np.tri(*corr.shape).T
sns.heatmap(corr.abs(), mask=mask, annot=True, annot_kws={"size": 9})
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show()
n_fts = len(data.columns)
colors = cm.rainbow(np.linspace(0, 1, n_fts))
data.drop('deposit',axis=1).corrwith(data.deposit).sort_values(ascending=True).plot(kind='barh',
color=colors, figsize=(12, 6))
plt.title('Correlation to Target (deposit)')
plt.show()
print('\n',data.drop('deposit',axis=1).corrwith(data.deposit).sort_values(ascending=False))
Logistic Regression with one independent variable¶
Example logistic regression equation:
$$y = \frac{e^{(\beta_0 + \beta_1*x)}}{(1 + e^{(\beta_0 + \beta_1*x)})}$$Where $y$ is the predicted output, $e$ is the base of the natural logarithms or the np.exp() function, $\beta_0$ is the bias or intercept term and $\beta_1$ is the coefficient for the single input value $(x)$. Each column in your input data has an associated $\beta$ coefficient (a constant real value) that must be learned from the training data.
We are going to begin with the simplest possible logistic model, using just one independent variable or feature, the duration.
y_simple = data['deposit']
x_n = 'duration'
x_c = data[x_n].values
with pm.Model() as model_simple:
# random variables for the coefficient with
# uninformative priors for each parameter
α = pm.Normal('α', mu=0, sd=10)
β = pm.Normal('β', mu=0, sd=10)
# Transform random variables into vector of probabilities
μ = α + pm.math.dot(x_c, β)
θ = pm.Deterministic('θ', pm.math.sigmoid(μ))
# The decision boundary
db = pm.Deterministic('db', -α/β)
# Bernoulli random vector with probability of success
# given by sigmoid function and actual data as observed
y = pm.Bernoulli(name='logit', p=θ, observed=y_simple)
trace_simple = pm.sample(1000, tune=1000, chains=4, init = 'adapt_diag', cores=5)
model_simple.model
The command pm.model_to_graphviz(manual_logistic_model) produces the plate notation displayed below.
It shows the unobserved parameters as light and the observed elements as dark circles. The rectangle indicates the number of repetitions of the observed model element implied by the data included in the model definition.
pm.model_to_graphviz(model_simple)
theta = trace_simple['θ'].mean(axis=0)
idx = np.argsort(x_c)
plt.plot(x_c[idx], theta[idx], color='red', lw=3)
plt.vlines(trace_simple['db'].mean(), 0, 1, color='k', ls='--')
plt.scatter(x_c, np.random.normal(y_simple, 0.02), marker='.', alpha=0.5,
color=[f'C{x}' for x in y_simple])
plt.xlabel(x_n)
plt.ylabel('θ', rotation=0)
locs, _ = plt.xticks()
plt.xticks(locs, np.round(locs + x_c.mean(), 1));
The above plot shows non deposit versus deposit $(y = 0, y = 1)$. The S-shaped (red) line is the mean value of $\theta$ (sigmoid function). This line can be interpreted as the probability of a deposit, given that we know that the last time contact duration (the value of the duration). The decision boundary is represented as a (black) vertical line. According to the decision boundary, the values of duration to the left correspond to $y = 0$ (non deposit), and the values to the right to $y = 1$ (deposit).
Create a data frame with trace summary statistics.¶
az.summary(trace_simple, var_names=['α', 'β', 'db'])
mean: Trace mean
sd: Trace standard deviation
mcse: Markov Chain Standard Error statistic
ess: Estimate of the effective sample size
r_hat: The R-hat diagnostic tests for lack of convergence by comparing the variance between multiple chains to the variance within each chain. If convergence has been achieved, the between-chain and within-chain variances should be identical. To be most effective in detecting evidence for nonconvergence, each chain should have been initialized to starting values that are dispersed relative to the target distribution.
Posterior Predictive Checks¶
PPCs are very useful for examining how well a model fits the data. They do so by generating data from the model using parameters from draws from the posterior. We use the function pm.sample_ppc for this purpose and obtain $n$ samples for each observation (the GLM module automatically names the outcome $y$):
ppc = pm.sample_ppc(trace_simple, model=model_simple, samples=500)
preds = np.rint(ppc['logit'].mean(axis=0)).astype('int')
y_score = np.mean(ppc['logit'], axis=0)
print('Accuracy of the simplest model:', accuracy_score(data['deposit'], preds))
print('AUC score of the simplest model:', roc_auc_score(data['deposit'], y_score))
Models¶
simple_model = 'deposit ~ duration + pdays + previous'
full_model = 'deposit ~ age + job + marital + default + day + month + duration + pdays + previous + education + balance + loan + poutcome + campaign + housing + contact'
MAP Inference¶
A probabilistic program consists of observed and unobserved random variables (RVs). We define the observed RVs via likelihood distributions and unobserved RVs via prior distributions. PyMC3 includes numerous probability distributions for this purpose.
The PyMC3 library makes it very straightforward to perform approximate Bayesian inference for logistic regression. Logistic regression models the probability that individual $i$ subscribes to a deposit based on $k$ features:
$$ p(y_i = 1 \mid \beta) = \sigma (\beta_0 + \beta_1 x_{i1} + \dots + \beta_k x_{ik}) $$Where $\sigma$ is the logistic function: $$ \sigma(t) = \frac{1}{1 + e^{-1}} $$
Manual Model Specification¶
We will use the context manager with to define a manual_logistic_model that we can refer to later as a probabilistic model:
- The random variables for the unobserved parameters for intercept and $3$ features are expressed using uninformative priors that assume normal distributions with mean $0$ and standard deviation of $100$.
- The likelihood combines the parameters with the data according to the specification of the logistic regression.
- The outcome is modeled as a Bernoulli RV with success probability given by the likelihood.
with pm.Model() as manual_logistic_model:
# random variables for coefficients with
# uninformative priors for each parameter
intercept = pm.Normal('intercept', 0, sd=100)
beta_1 = pm.Normal('beta_1', 0, sd=100)
beta_2 = pm.Normal('beta_2', 0, sd=100)
beta_3 = pm.Normal('beta_3', 0, sd=100)
# Transform random variables into vector of probabilities p(y_i=1)
# according to logistic regression model specification.
likelihood = pm.invlogit(intercept + beta_1 * data.duration + beta_2 * data.pdays + beta_3 * data.previous)
# Bernoulli random vector with probability of success
# given by sigmoid function and actual data as observed
pm.Bernoulli(name='logit', p=likelihood, observed=data.deposit)
manual_logistic_model.model
pm.model_to_graphviz(manual_logistic_model)
MAP Estimate¶
Maximum a posteriori probability (MAP) estimation leverages that the evidence is a constant factor that scales the posterior to meet the requirements for a probability distribution. Since the evidence does not depend on $θ$, the posterior distribution is proportional to the product of the likelihood and the prior. Hence, MAP estimation chooses the value of $θ$ that maximizes the posterior given the observed data and the prior belief, that is, the mode of the posterior.
$$ \theta_{MAP} = \operatorname*{arg\,max}_\theta P(X \mid \theta) P(\theta) $$We obtain point MAP estimates for the three parameters using the just defined model’s .find_MAP() method:
with manual_logistic_model:
# compute maximum a-posteriori estimate
# for logistic regression weights
manual_map_estimate = pm.find_MAP()
def print_map(result):
return pd.Series({k: np.asscalar(v) for k, v in result.items()})
print_map(manual_map_estimate)
GLM Model¶
PyMC3 includes numerous common models so that we can usually leave the manual specification for custom applications.
The following code defines the same logistic regression as a member of the Generalized Linear Models (GLM) family using the formula format inspired by the statistical language R and ported to python by the patsy library:
with pm.Model() as logistic_model:
pm.glm.GLM.from_formula(simple_model,
data,
family=pm.glm.families.Binomial())
pm.model_to_graphviz(logistic_model)
PyMC3 solves the optimization problem of finding the posterior point with the highest density using the quasi-Newton Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm but offers several alternatives provided by the scipy library. The result is virtually identically to the corresponding statsmodels estimate:
model = smf.logit(formula=simple_model, data=data[['deposit', 'duration', 'pdays', 'previous']])
result = model.fit()
print(result.summary())
print_map(manual_map_estimate)
result.params
Markov Chain Monte Carlo¶
Markov chains are stochastic models that describe sequences of possible events. Each event comes from a set of outcomes, and each outcome determines which outcome occurs next, according to a fixed set of probabilities. An important feature of Markov chains is that they are memoryless: everything that you would possibly need to predict the next event is available in the current state, and no new information comes from knowing historical events.
Monte Carlo methods rely on repeated random sampling to approximate results that may be deterministic, but that does not permit an analytic, exact solution.
Many algorithms apply the Monte Carlo method to a Markov Chain, and generally proceed as follows:
- Start at the current position.
- Draw a new position from a proposal distribution.
- Evaluate the probability of the new position in light of data and prior distributions:
- If sufficiently likely, move to the new position
- Otherwise, remain at the current position
- Repeat from step 1.
- After a given number of iterations, return all accepted positions.
Define the Model¶
We will use a slightly more complicated model to illustrate Markov chain Monte Carlo inference:
full_model = 'deposit ~ age + job + marital + default + day + month + duration + pdays + previous + education + balance + loan + poutcome + campaign + housing + contact'
with pm.Model() as logistic_model:
pm.glm.GLM.from_formula(formula=full_model,
data=data,
family=pm.glm.families.Binomial())
pm.model_to_graphviz(logistic_model)
Hamiltonian Monte Carlo – going NUTS¶
By default, PyMC3 automatically selects the most efficient sampler and initializes the sampling process for efficient convergence. For a continuous model, PyMC3 chooses the NUTS sampler. It also runs variational inference via ADVI to find good starting parameters for the sampler. One among several alternatives is to use the MAP estimate.
Hamiltonian Monte Carlo (HMC) is a hybrid method that leverages the first-order derivative information of the gradient of the likelihood to propose new states for exploration and overcome some of the challenges of MCMC. In addition, it incorporates momentum to efficiently jump around the posterior. As a result, it converges faster to a high-dimensional target distribution than simpler random-walk Metropolis or Gibbs sampling.
To see what the convergence looks like, we first draw $1,000$ samples after tuning the sampler for $1,000$ iterations that will be discarded. The sampling process can be parallelized for multiple chains using the cores argument (except when using GPU).
with logistic_model:
trace = pm.sample(tune=1000, draws=1000, chains=4, init = 'adapt_diag', cores=5)
Inspect Trace¶
pm.plot_trace(trace);
- On the left, we have a KDE plot, — for each parameter value on the x-axis we get a probability on the y-axis that tells us how likely that parameter value is. The maximum posterior estimate of each variable (the peak in the left side distributions) is very close to the true parameters.
- On the right, we get the individual sampled values at each step during the sampling. From the trace plot, we can visually get the plausible values from the posterior. Our sampling chains for the individual parameters (left) seem well converged and stationary (there are no large drifts or other odd patterns).
Plot joint distribution of parameters.¶
One of the major benefits of Bayesian data analysis is that we can be explicit about our uncertainty. Maximum likelihood returns a number, but how certain can we be that we found the right number? Instead, Bayesian inference returns a distribution over parameter values.
temp = pd.DataFrame(dict(job =trace['job'], edu = trace['education']))
kdeplot = sns.jointplot(data=temp, x='edu', y='job', kind="kde", cmap='jet', cbar=True, n_levels=100,
marginal_kws={'color': 'blue'}).annotate(stats.pearsonr)
kdeplot.fig.set_size_inches(9, 7)
plt.subplots_adjust(left=0.1, right=0.8, top=0.9, bottom=0.1)
pos_joint_ax = kdeplot.ax_joint.get_position()
pos_marg_x_ax = kdeplot.ax_marg_x.get_position()
kdeplot.ax_joint.set_position([pos_joint_ax.x0, pos_joint_ax.y0, pos_marg_x_ax.width, pos_joint_ax.height])
kdeplot.fig.axes[-1].set_position([.83, pos_joint_ax.y0, .07, pos_joint_ax.height])
plt.show()
Interpreting Model Coefficients¶
Here we fit a logistic regression model using MLE via the statsmodels.formula library and exctract the p-values and coefficients. We will also calculate the odds ratio of the coefficients to try and interpret the models feature importance.
tmp = data.copy()
tmp['deposit'] = data['deposit']
model = smf.logit(formula=full_model, data=tmp)
result = model.fit()
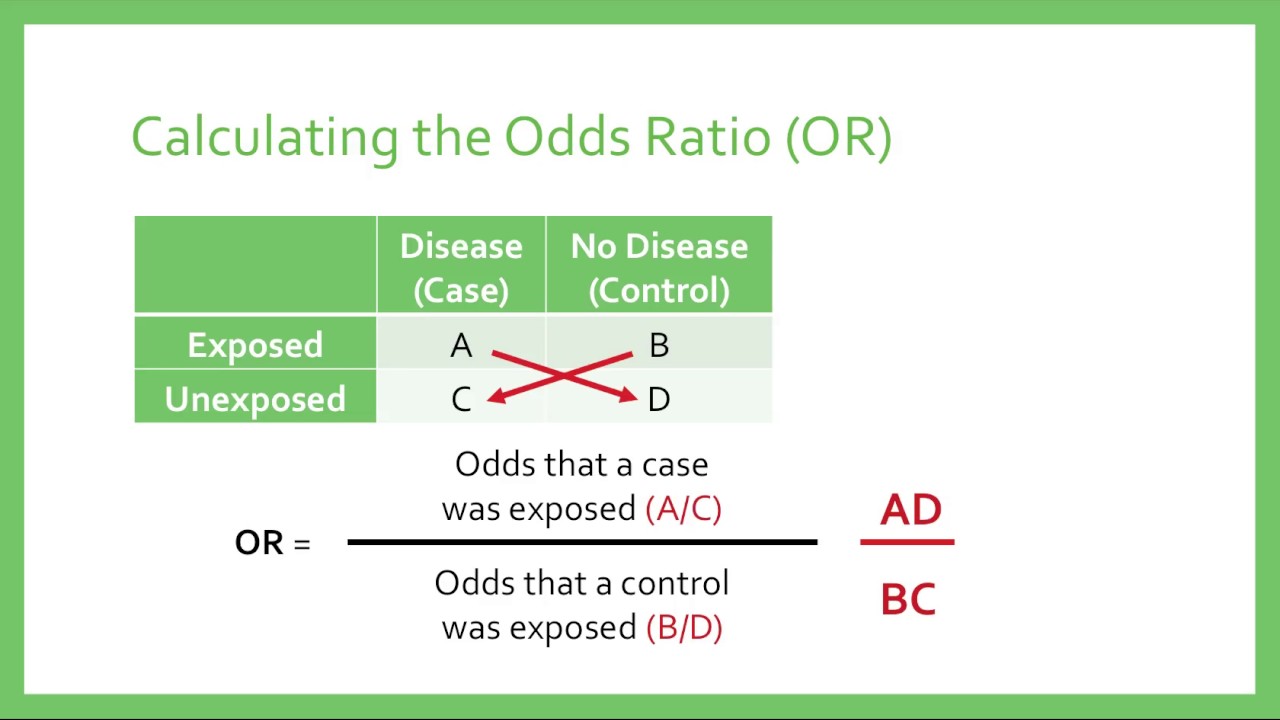
An odds ratio (OR) is a measure of association between a certain property $A$ and a second property $B$ in a population. Specifically, it tells you how the presence or absence of property $A$ has an effect on the presence or absence of property $B$. The OR is also used to figure out if a particular exposure (like eating processed meat) is a risk factor for a particular outcome (such as colon cancer), and to compare the various risk factors for that outcome. As long as you have two properties you think are linked, you can calculate the odds.
You have two choices for the formula: $$\frac{(a \div c)}{(b \div d)}$$
or, equivalently: $$\frac{(a \times d)}{(b \times c)}$$
- $OR = 1$ indicates exposure does not affect odds of event occurrence
- $OR > 1$ indicates increased occurrence of event
- $OR < 1$ indicates decreased occurrence of event (protective exposure)
We can get the odds ratio of the model coefficients by exponentiating the coefficients.
log_df = pd.DataFrame(dict(coefs = result.params[1:], p_vals = result.pvalues[1:]), index=data.columns)
log_df['odds'] = np.exp(log_df['coefs'])
log_df['Pct_odds_increase'] = (log_df['odds'] - 1) * 100
log_df = log_df.sort_values('odds', ascending=False)
mask = log_df.p_vals <= 0.05
log_df[mask]
Each curve shows how the probability of subscribing to a term deposit changes with duration, given this customer owns a house.
The red curve represents success, the green curve represents unknown and, the blue failure poutcomes (outcome of the previous marketing campaign). For all three poutcomes levels, the probability of subscribing a term deposit increases with duration until approximately duration (last contact duration, in seconds) $0$, when the probability begins to decrease.
We are plotting $100$ different curves for each level of poutcomes. Each curve is a draw from our posterior distribution.
def lm_full(trace, duration, poutcome, housing):
shape = np.broadcast(duration, poutcome, housing).shape
x_norm = np.asarray([np.broadcast_to(x, shape) for x in [duration, poutcome, housing]])
return 1 / (1 + np.exp(-(trace['Intercept'] +
trace['duration']*x_norm[0] +
trace['poutcome']*x_norm[1] +
trace['housing']*x_norm[2])))
lm = lambda x, samples: lm_full(samples, x, 1, 1)
lm2 = lambda x, samples: lm_full(samples, x,2, 1)
lm3 = lambda x, samples: lm_full(samples, x, 4, 1)
min_age = min(data.duration)
max_age = max(data.duration)
# Plot the posterior predictive distributions of P(deposit = yes) vs. duration
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(
min_age, max_age, 1000), lm=lm, samples=100, color="blue", alpha=.7)
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(
min_age, max_age, 1000), lm=lm2, samples=100, color="green", alpha=.7)
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(
min_age, max_age, 1000), lm=lm3, samples=100, color="red", alpha=.7)
blue_line = mlines.Line2D(['lm'], [], color='b', label='failure')
green_line = mlines.Line2D(['lm2'], [], color='g', label='unknown')
red_line = mlines.Line2D(['lm3'], [], color='r', label='success')
plt.legend(handles=[blue_line, green_line, red_line], loc='lower right')
plt.ylabel("P(deposit = yes)")
plt.xlabel("duration")
plt.show()
pm.trace_to_dataframe(trace).info()
with open(model_path / 'logistic_model_mh.pkl', 'wb') as buff:
pickle.dump({'model': logistic_model, 'trace': trace}, buff)
pm.summary(trace)
draws = 100
trace_df = pm.trace_to_dataframe(trace).assign(
chain=lambda x: x.index // draws)
trace_df.info()
Persist Results¶
with open(model_path / 'logistic_model_nuts.pkl', 'wb') as buff:
pickle.dump({'model': logistic_model,
'trace': trace}, buff)
with open(model_path / 'logistic_model_nuts.pkl', 'rb') as buff:
data0 = pickle.load(buff)
logistic_model, trace_NUTS = data0['model'], data0['trace']
Combine Traces¶
draws = 10000
df = pm.trace_to_dataframe(trace_NUTS).iloc[200:].reset_index(
drop=True).assign(chain=lambda x: x.index // draws)
trace_df = pd.concat([trace_df.assign(samples=100),
df.assign(samples=10000)])
trace_df.info()
Visualize both traces¶
trace_df_long = pd.melt(trace_df, id_vars=['samples', 'chain'])
trace_df_long.info()
Convergence¶
We can visualize the samples over time and their distributions to check the quality of the results. The following charts show the posterior distributions after an initial $100$ and an additional $10,000$ samples, respectively, and illustrate how convergence implies that multiple chains identify the same distribution. The pm.trace_plot() function shows the evolution of the samples as well.
g = sns.FacetGrid(trace_df_long, col='variable', row='samples',
hue='chain', sharex='col', sharey=False)
g = g.map(sns.distplot, 'value', hist=False, rug=False)
Estimate Odds Ratio¶
b = trace['duration']
lb, ub = np.percentile(b, 2.5), np.percentile(b, 97.5)
lb, ub = np.exp(lb), np.exp(ub)
print(f'P({lb:.3f} < Odds Ratio < {ub:.3f}) = 0.95')
We can interpret something along those lines: "With probability $0.95$ the odds ratio is greater than $4.985$ and less than $5.725$, so the duration effect takes place because a person with a longer contact duration has at least $4.985$ higher probability to subscribe to a term deposit than a person with a lower duration, while holding all the other variables constant.
Computing Credible Intervals¶
We can compute the credible intervals, the Bayesian counterpart of confidence intervals, as percentiles of the trace. The resulting boundaries reflect our confidence about the range of the parameter value for a given probability threshold, as opposed to the number of times the parameter will be within this range for a large number of trials.
fig, ax = plt.subplots(figsize=(8, 4))
sns.distplot(np.exp(b), axlabel='Odds Ratio', ax=ax)
ax.set_title(f'Credible Interval: P({lb:.3f} < Odds Ratio < {ub:.3f}) = 0.95')
ax.axvspan(lb, ub, alpha=0.25, color='gray');
Variational Inference¶
Variational Inference (VI) is a machine learning method that approximates probability densities through optimization. In the Bayesian context, it approximates the posterior distribution as follows:
- Select a parametrized family of probability distributions
- Find the member of this family closest to the target, as measured by Kullback-Leibler divergence
Compared to MCMC, Variational Bayes tends to converge faster and scales to large data better. While MCMC approximates the posterior with samples from the chain that will eventually converge arbitrarily close to the target, variational algorithms approximate the posterior with the result of the optimization, which is not guaranteed to coincide with the target.
Variational Inference is better suited for large datasets and to quickly explore many models.In contrast, MCMC will deliver more accurate results on smaller datasets or when time and computational resources pose fewer constraints.
Run Automatic Differentation Variational Inference (ADVI)¶
The interface for variational inference is very similar to the MCMC implementation. We just use the fit() instead of the sample() function, with the option to include an early stopping CheckParametersConvergence callback if the distribution-fitting process converged up to a given tolerance:
with logistic_model:
callback = CheckParametersConvergence(diff='absolute')
approx = pm.fit(n=100000, callbacks=[callback])
Persist Result¶
with open(model_path / 'logistic_model_advi.pkl', 'wb') as buff:
pickle.dump({'model': logistic_model,
'approx': approx}, buff)
Sample from approximated distribution¶
We can draw samples from the approximated distribution to obtain a trace object as above for the MCMC sampler:
trace_advi = approx.sample(2000)
# pm.summary(trace_advi).to_csv(model_path / 'trace_advi.csv')
Visualize the covariance structure of the models¶
az.plot_pair(trace_NUTS, figsize=(10, 10), kind='kde', divergences=True);
Let us visualize the covariance structure of the ADVI model
az.plot_pair(trace_advi, figsize=(10, 10), kind='kde', divergences=True);
Clearly, ADVI does not capture (as expected) the interactions between variables because of the mean field approximation, and so it underestimates the overall variance.
Model Diagnostics¶
Bayesian model diagnostics includes validating that the sampling process has converged and consistently samples from high-probability areas of the posterior, and confirming that the model represents the data well.
For high-dimensional models with many variables, it becomes cumbersome to inspect numerous traces. When using NUTS, the energy plot helps to assess problems of convergence. It summarizes how efficiently the random process explores the posterior. The plot shows the energy and the energy transition matrix that should be well matched as in the below example.
Energy Plot¶
When using NUTS, the energy plot helps to assess problems of convergence. It summarizes how efficiently the random process explores the posterior. The plot shows the energy and the energy transition matrix, which should be well-matched.
pm.energyplot(trace_NUTS);
Forest Plot¶
A forest plot, also known as a blobbogram, is a graphical display of estimated results from a number of scientific studies addressing the same question, along with the overall results. It was developed for use in medical research as a means of graphically representing a meta-analysis of the results of randomized controlled trials.
az.plot_forest([trace_advi, trace_NUTS], model_names=['trace_advi', 'trace_NUTS']);
Posterior Plot¶
pm.plot_posterior(trace_NUTS);
Model selection using Widely-applicable Information Criterion (WAIC)¶
WAIC (Watanabe 2010) is a fully Bayesian criterion for estimating out-of-sample expectation, using the computed log pointwise posterior predictive density (LPPD) and correcting for the effective number of parameters to adjust for overfitting.
One question that was immediately asked was what effect does campaign have on the model, and why should it be $\text{campaign}^2$ versus campaign? We’ll run the model with a few changes to see what effect increasing polynomial complexity has on this model in terms of WAIC.
def run_models(df, upper_order=5):
models, traces = OrderedDict(), OrderedDict()
for k in range(1,upper_order+1):
nm = 'k{}'.format(k)
fml = create_poly_modelspec(k)
with pm.Model() as models[nm]:
print('\nRunning: {}'.format(nm))
pm.glm.GLM.from_formula(fml, df,
family=pm.glm.families.Binomial())
traces[nm] = pm.sample(1000, tune=1000, chains=4, init = 'adapt_diag', cores=5)
return models, traces
def create_poly_modelspec(k=1):
return ('deposit ~ age + job + marital + default + day + month + duration + pdays + previous + education + balance + loan + poutcome + campaign + housing + contact' + ' '.join(['+ np.power(campaign,{})'.format(j)
for j in range(2,k+1)])).strip()
models_lin, traces_lin = run_models(data, 4)
model_trace_dict = dict()
ks = ['k1', 'k2', 'k3', 'k4']
for nm in ks:
models_lin[nm].name = nm
model_trace_dict.update({models_lin[nm]: traces_lin[nm]})
dfwaic = pm.compare(model_trace_dict, ic='WAIC')
dfwaic = dfwaic.reset_index(drop=True)
dfwaic['names'] = ks
dfwaic = dfwaic.sort_values('rank')
dfwaic.index = dfwaic.names
dfwaic
- We prefer the model(s) with lower WAIC.
Next we use the pm.compareplot function takes the output of pm.compare and produces a summary plot.
pm.compareplot(dfwaic);
- The empty circle represents the values of WAIC and the black error bars associated with them are the values of the standard deviation of WAIC.
- The value of the lowest WAIC is also indicated with a vertical dashed grey line to ease comparison with other WAIC values.
- The filled in black dots are the in-sample deviance of each model, which for WAIC is 2 pWAIC from the corresponding WAIC value.
- For all models except the top-ranked one, we also get a triangle, indicating the value of the difference of WAIC between that model and the top model, and a grey error bar indicating the standard error of the differences between the top-ranked WAIC and WAIC for each model.
This confirms that the original model is better than the models with increasing polynomial complexity.
Posterior Predictive Checks¶
PPCs are very useful for examining how well a model fits the data. They do so by generating data from the model using parameters from draws from the posterior. We use the function pm.sample_ppc for this purpose and obtain $n$ samples for each observation (the GLM module automatically names the outcome $y$):
ppc = pm.sample_ppc(trace_NUTS, samples=500, model=logistic_model)
ppc['y'].shape
Check AUC Score¶
y_score = np.mean(ppc['y'], axis=0)
pred_scores = dict(y_true=data.deposit,y_score=y_score)
preds = np.rint(ppc['y'].mean(axis=0)).astype('int')
print('Accuracy of the full model: ', accuracy_score(data.deposit, preds))
print('AUC of the full model: ', roc_auc_score(**pred_scores))
Prediction¶
Follows PyMC3 docs
Predictions use theano’s shared variables to replace the training data with test data before running posterior predictive checks. To facilitate visualization, we create the train and test datasets, and convert the former to a shared variable. Note that we need to use numpy arrays and provide a list of column labels:
Train-test split¶
X = data.drop('deposit', axis=1)
y = data.deposit
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
labels = X_train.columns
Create shared theano variable¶
X_shared = theano.shared(X_train.values)
Define logistic model¶
with pm.Model() as logistic_model_pred:
pm.glm.GLM(x=X_shared, labels=labels,
y=y_train, family=pm.glm.families.Binomial())
Run NUTS sampler¶
with logistic_model_pred:
pred_trace = pm.sample(draws=1000, tune=1000, chains=4, cores=5, init='adapt_diag')
Replace shared variable with test set¶
We then run the sampler as before, and apply the pm.sample_ppc function to the resulting trace after replacing the train with test data:
X_shared.set_value(X_test)
ppc = pm.sample_ppc(pred_trace,
model=logistic_model_pred,
samples=5000)
AUC Score¶
y_score = np.mean(ppc['y'], axis=0)
preds = np.rint(ppc['y'].mean(axis=0)).astype('int')
print('Accuracy on test data: ', accuracy_score(y_test, preds))
print('AUC on test data: ', roc_auc_score(y_score=y_score, y_true=y_test))
Thresholding probabilities¶
from plot_utils import plot_thresholds, comp_conf_matrix
plot_thresholds(X_test, y_test, y_score, name='Bayesian Logistic Regression', fig_x=13, fig_y=4,
sizes=[0.55, -95, -45])
g_ts_pred = np.where(y_score > 0.44, 1, 0)
f1_ts_pred = np.where(y_score > 0.40, 1, 0)
prl_ts_pred = np.where(y_score > 0.50, 1, 0)
f1_ts_cm = np.around(confusion_matrix(y_test, f1_ts_pred, normalize='true'), decimals=3)
g_ts_cm = np.around(confusion_matrix(y_test, g_ts_pred, normalize='true'), decimals=3)
prl_ts_cm = np.around(confusion_matrix(y_test, prl_ts_pred, normalize='true'), decimals=3)
no_ts_cm = np.around(confusion_matrix(y_test, preds, normalize='true'), decimals=3)
comp_conf_matrix(mtx1=no_ts_cm, mtx2=f1_ts_cm, labels=['deposit', 'no deposit'],
titles=['No Threshold', 'F1 Thresholded'], sizes=[10, 4])
comp_conf_matrix(mtx1=prl_ts_cm, mtx2=g_ts_cm, labels=['deposit', 'no deposit'],
titles=['PRL Thresholded', 'G Thresholded'], sizes=[10, 4])