Deep Learning Performance Part 3 Batch Normalization, Dropout and Noise¶
Batch Normalization¶
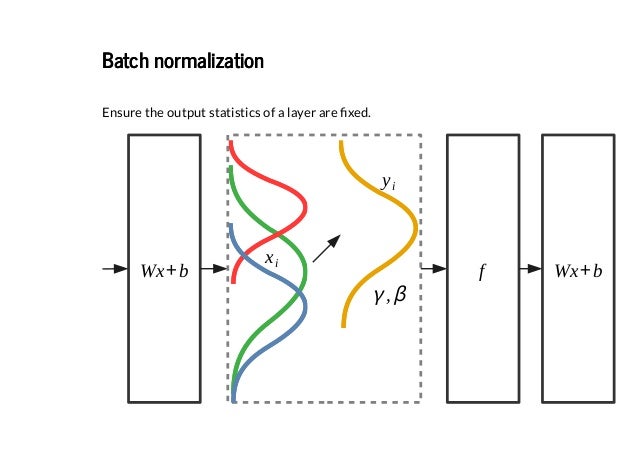
Training deep neural networks with tens of layers is challenging as they can be sensitive to the initial random weights and configuration of the learning algorithm.
One possible reason for this difficulty is the distribution of the inputs to layers deep in the network may change after each mini-batch when the weights are updated. This can cause the learning algorithm to forever chase a moving target. This change in the distribution of inputs to layers in the network is referred to the technical name internal covariate shift.
Batch normalization is a technique for training very deep neural networks that standardizes the inputs to a layer for each mini-batch. This has the effect of stabilizing the learning process and dramatically reducing the number of training epochs required to train deep networks.
Batch normalization has the effect of dramatically accelerating the training process of a neural network, and in some cases improves the performance of the model providing a slight regularization effect.
Tips for Using Batch Normalization¶
Use With Different Network Types¶
- It can be used with most network types, such as Multilayer Perceptrons, Convolutional Neural Networks and Recurrent Neural Networks.
Probably Use Before the Activation¶
It may be more appropriate to use batch normalization after the activation function if for s-shaped functions like the hyperbolic tangent and logistic function.
It may be appropriate before the activation function for activations that may result in non-Gaussian distributions like the rectified linear activation function.
Use Large Learning Rates¶
Using batch normalization makes the network more stable during training. This may require the use of much larger than normal learning rates, that in turn may further speed up the learning process.
The faster training also means that the decay rate used for the learning rate may be increased.
Alternate to Data Preparation¶
If the mean and standard deviations calculated for each input feature are calculated over the mini-batch instead of over the entire training dataset, then the batch size must be sufficiently representative of the range of each variable.
It may not be appropriate for variables that have a data distribution that is highly non-Gaussian, in which case it might be better to perform data scaling as a pre-processing step.
Less Sensitive to Weight Initialization¶
Keras Weight Initialization
The neural network needs to start with some random weights and then iteratively update them to better values. The term kernel_initializer is a fancy term for which statistical distribution or function to use for initialising the weights. In case of statistical distribution, the library will generate numbers from that statistical distribution and use as starting weights. Choices for initialization documented here
Deep neural networks can be quite sensitive to the technique used to initialize the weights prior to training.
The stability to training brought by batch normalization can make training deep networks less sensitive to the choice of weight initialization method.
Don’t Use With Dropout¶
Batch normalization offers some regularization effect, reducing generalization error, perhaps no longer requiring the use of dropout for regularization.
The statistics used to normalize the activations of the prior layer may become noisy given the random dropping out of nodes during the dropout procedure.
BatchNormalization in Keras¶
Keras provides support for batch normalization via the BatchNormalization layer.
For example:
from keras.layers import BatchNormalization
bn = BatchNormalization()
The layer will transform inputs so that they are standardized, meaning that they will have a mean of zero and a standard deviation of one.
During training, the layer will keep track of statistics for each input variable and use them to standardize the data.
Further, the standardized output can be scaled using the learned parameters of Beta and Gamma that define the new mean and standard deviation for the output of the transform. The layer can be configured to control whether these additional parameters will be used or not via the center and scale attributes respectively. By default, they are enabled.
The statistics used to perform the standardization, e.g. the mean and standard deviation of each variable, are updated for each mini batch and a running average is maintained.
A momentum argument allows you to control how much of the statistics from the previous mini batch to include when the update is calculated. By default, this is kept high with a value of $0.99$. This can be set to $0.0$ to only use statistics from the current mini-batch, as described in the original paper.
bn = BatchNormalization(momentum=0.0)
At the end of training, the mean and standard deviation statistics in the layer at that time will be used to standardize inputs when the model is used to make a prediction.
The default configuration estimating mean and standard deviation across all mini batches is probably sensible.
BatchNormalization in Models¶
Batch normalization can be used at most points in a model and with most types of deep learning neural networks. The BatchNormalization layer can be added to your model to standardize raw input variables or the outputs of a hidden layer.
Batch normalization is not recommended as an alternative to proper data preparation for your model. Nevertheless, when used to standardize the raw input variables, the layer must specify the input_shape argument; for example:
BatchNormalization(input_shape=(2,))
Use Before or After the Activation Function¶
The BatchNormalization layer can be used to standardize inputs before or after the activation function of the previous layer.
The original paper that introduced the method suggests adding batch normalization before the activation function of the previous layer, for example:
from keras.models import Sequential
from keras.layers import Dense, Activation
model = Sequential()
model.add(Dense(32))
model.add(BatchNormalization())
model.add(Activation('relu'))
Some reported experiments suggest better performance when adding the batch normalization layer after the activation function of the previous layer; for example:
model = Sequential()
model.add(Dense(32, activation='relu'))
model.add(BatchNormalization())
If time and resources permit, it may be worth testing both approaches on your model and use the approach that results in the best performance.
Let’s take a look at how batch normalization can be used with some common network types.
MLP Batch Normalization¶
The example below adds batch normalization after the activation function between Dense hidden layers.
model.add(Dense(32, activation='relu'))
model.add(BatchNormalization())
model.add(Dense(1))
CNN Batch Normalization¶
The example below adds batch normalization after the activation function between a convolutional and max pooling layers.
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
model.add(Conv2D(32, (3,3), activation='relu'))
model.add(Conv2D(32, (3,3), activation='relu'))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dense(1))
RNN Batch Normalization¶
The example below adds batch normalization after the activation function between an LSTM and Dense hidden layers.
from keras.layers import LSTM
model.add(LSTM(32))
model.add(BatchNormalization())
model.add(Dense(1))
BatchNormalization Binary Classification Problem¶
We will demonstrate how to use batch normalization to accelerate the training of an MLP on a simple binary classification problem.
We will use a standard binary classification problem that defines two two-dimensional concentric circles of observations, one circle for each class.
Each observation has two input variables with the same scale and a class output value of either $0$ or $1$. This dataset is called the circles dataset because of the shape of the observations in each class when plotted.
We can use the sklearn make_circles() function to generate observations from this problem. We will add noise to the data and seed the random number generator so that the same samples are generated each time the code is run.
from sklearn.datasets import make_circles
import numpy as np
import matplotlib.pyplot as plt
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
fig, ax = plt.subplots(figsize=(10,6))
# select indices of points with each class label
for i in range(2):
samples_ix = np.where(y == i)
plt.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i), s=50, alpha=0.5)
plt.legend()
plt.show()
This is a good test problem because the classes cannot be separated by a line, e.g. are not linearly separable, requiring a nonlinear method such as a neural network to address.
Multilayer Perceptron Model¶
We can develop a Multilayer Perceptron model, or MLP, as a baseline for this problem.
First, we will split the $1,000$ generated samples into a train and test dataset, with $500$ examples in each. This will provide a sufficiently large sample for the model to learn from and an equally sized (fair) evaluation of its performance.
from keras.optimizers import SGD
import time
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
start_time = time.time()
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
end_time = time.time() - start_time
min_ = end_time/60
hrs = min_/60
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.title(f'Runtime Hrs: {round(hrs,3)}, Min: {round(min_,3)}, Sec: {round(end_time,3)}')
plt.legend()
plt.show()
This result, and specifically the dynamics of the model during training, provide a baseline that can be compared to the same model with the addition of batch normalization.
MLP With Batch Normalization¶
The expectation is that the addition of batch normalization would accelerate the training process, offering similar or better classification accuracy of the model in fewer training epochs. Batch normalization is also reported as providing a modest form of regularization, meaning that it may also offer a small reduction in generalization error demonstrated by a small increase in classification accuracy on the holdout test dataset.
A new BatchNormalization layer can be added to the model after the hidden layer before the output layer. Specifically, after the activation function of the prior hidden layer.
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(BatchNormalization())
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
start_time = time.time()
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
end_time = time.time() - start_time
min_ = end_time/60
hrs = min_/60
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.title(f'Runtime Hrs: {round(hrs,3)}, Min: {round(min_,3)}, Sec: {round(end_time,3)}')
plt.legend()
plt.show()
In this case, we can see that the model has learned the problem faster than the model in the previous section without batch normalization. Specifically, we can see that classification accuracy on the train and test datasets leaps above 80% within the first $20$ epochs, as opposed to $30$-to-$40$ epochs in the model without batch normalization.
We can see lower performance on the training dataset than the test dataset: scores on the training dataset that are lower than the performance of the model at the end of the training run. This is likely the effect of the input collected and updated each mini-batch.
We can also try a variation of the model where batch normalization is applied prior to the activation function of the hidden layer, instead of after the activation function.
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, kernel_initializer='he_uniform'))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
start_time = time.time()
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
end_time = time.time() - start_time
min_ = end_time/60
hrs = min_/60
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.title(f'Runtime Hrs: {round(hrs,3)}, Min: {round(min_,3)}, Sec: {round(end_time,3)}')
plt.legend()
plt.show()
The plot shows the model learning perhaps at the same pace as the model without batch normalization, but the performance of the model on the training dataset is much worse, hovering around $70\%$ to $75\%$ accuracy, again likely an effect of the statistics collected and used over each mini-batch.
At least for this model configuration on this specific dataset, it appears that batch normalization is more effective after the rectified linear activation function.
Extensions to explore.¶
- Without Beta and Gamma. Update the example to not use the beta and gamma parameters in the batch normalization layer and compare results.
- Without Momentum. Update the example to not use momentum in the batch normalization layer during training and compare results.
- Input Layer. Update the example to use batch normalization after the input to the model and compare results.
Dropout¶

Deep learning neural networks are likely to quickly overfit a training dataset with few examples.
Ensembles of neural networks with different model configurations are known to reduce overfitting, but require the additional computational expense of training and maintaining multiple models.
A single model can be used to simulate having a large number of different network architectures by randomly dropping out nodes during training. This is called dropout and offers a very computationally cheap and remarkably effective regularization method to reduce overfitting and improve generalization error in deep neural networks of all kinds.
Randomly Drop Nodes¶
Dropout is a regularization method that approximates training a large number of neural networks with different architectures in parallel.
During training, some number of layer outputs are randomly ignored or dropped out. This has the effect of making the layer look-like and be treated-like a layer with a different number of nodes and connectivity to the prior layer. In effect, each update to a layer during training is performed with a different view of the configured layer.
Dropout has the effect of making the training process noisy, forcing nodes within a layer to probabilistically take on more or less responsibility for the inputs. This conceptualization suggests that perhaps dropout breaks-up situations where network layers co-adapt to correct mistakes from prior layers, in turn making the model more robust.
Dropout simulates a sparse activation from a given layer, which interestingly, in turn, encourages the network to actually learn a sparse representation as a side-effect. As such, it may be used as an alternative to activity regularization for encouraging sparse representations in autoencoder models.
Because the outputs of a layer under dropout are randomly subsampled, it has the effect of reducing the capacity or thinning the network during training. As such, a wider network, e.g. more nodes, may be required when using dropout.
How to Dropout¶
Dropout is implemented per-layer in a neural network.
It can be used with most types of layers, such as dense fully connected layers, convolutional layers, and recurrent layers such as the long short-term memory network layer. Dropout may be implemented on any or all hidden layers in the network as well as the visible or input layer. It is not used on the output layer.
A new hyperparameter is introduced that specifies the probability at which outputs of the layer are dropped out, or inversely, the probability at which outputs of the layer are retained. A common value is a probability of $0.5$ for retaining the output of each node in a hidden layer and a value close to $1.0$, such as $0.8$, for retaining inputs from the visible layer.
Dropout is not used after training when making a prediction with the fit network.
The weights of the network will be larger than normal because of dropout. Therefore, before finalizing the network, the weights are first scaled by the chosen dropout rate. The network can then be used to make predictions.
The rescaling of the weights can be performed at training time instead, after each weight update at the end of the mini-batch. This is sometimes called inverse dropout and does not require any modification of weights during training. Both the Keras and PyTorch deep learning libraries implement dropout in this way.
Tips for Using Dropout Regularization¶
Dropout Rate¶
The default interpretation of the dropout hyperparameter is the probability of training a given node in a layer, where $1.0$ means no dropout, and $0.0$ means no outputs from the layer.
A good value for dropout in a hidden layer is between $0.5$ and $0.8$. Input layers use a larger dropout rate, such as of $0.8$.
Use a Weight Constraint¶
Network weights will increase in size in response to the probabilistic removal of layer activations. Large weight size can be a sign of an unstable network.
To counter this effect a weight constraint can be imposed to force the norm (magnitude) of all weights in a layer to be below a specified value. For example, the maximum norm constraint is recommended with a value between $3-4$.
Dropout Regularization in Keras¶
The simplest form of dropout in Keras is provided by a Dropout core layer.
When created, the dropout rate can be specified to the layer as the probability of setting each input to the layer to zero. This is different from the definition of dropout rate from the papers, in which the rate refers to the probability of retaining an input.
Therefore, when a dropout rate of $0.8$ is suggested in a paper (retain $80\%$), this will, in fact, will be a dropout rate of $0.2$ (set $20\%$ of inputs to zero).
Below is an example of creating a dropout layer with a $50\%$ chance of setting inputs to zero.
from keras.layers import Dropout
layer = Dropout(0.5)
Dropout Regularization on Layers¶
The Dropout layer is added to a model between existing layers and applies to outputs of the prior layer that are fed to the subsequent layer.
For example:
from keras.layers import Dense
Dense(32)
Dropout(0.5)
Dense(32)
Dropout can also be applied to the visible layer, e.g. the inputs to the network.
This requires that you define the network with the Dropout layer as the first layer and add the input_shape argument to the layer to specify the expected shape of the input samples.
Dropout(0.5, input_shape=(2,))
CNN Dropout Regularization¶
Dropout can be used after convolutional layers (e.g. Conv2D) and after pooling layers (e.g. MaxPooling2D).
Often, dropout is only used after the pooling layers, but this is just a rough heuristic.
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
Conv2D(32, (3,3))
Conv2D(32, (3,3))
MaxPooling2D()
Dropout(0.5)
Dense(1)
In this case, dropout is applied to each element or cell within the feature maps.
An alternative way to use dropout with convolutional neural networks is to dropout entire feature maps from the convolutional layer which are then not used during pooling. This is called spatial dropout (or SpatialDropout).
Spatial Dropout is provided in Keras via the SpatialDropout2D layer (as well as 1D and 3D versions).
from keras.layers import SpatialDropout2D
Conv2D(32, (3,3))
Conv2D(32, (3,3))
SpatialDropout2D(0.5)
MaxPooling2D()
Dense(1)
RNN Dropout Regularization¶
The example below adds dropout between two layers: an LSTM recurrent layer and a dense fully connected layers.
from keras.layers import LSTM
LSTM(32)
Dropout(0.5)
Dense(1)
This example applies dropout to, in this case, $32$ outputs from the LSTM layer provided as input to the Dense layer.
Alternately, the inputs to the LSTM may be subjected to dropout. In this case, a different dropout mask is applied to each time step within each sample presented to the LSTM.
Dropout(0.5, input_shape=(5,))
LSTM(32)
Dense(1)
There is an alternative way to use dropout with recurrent layers like the LSTM. The same dropout mask may be used by the LSTM for all inputs within a sample. The same approach may be used for recurrent input connections across the time steps of the sample. This approach to dropout with recurrent models is called a Variational RNN.
Keras supports Variational RNNs (i.e. consistent dropout across the time steps of a sample for inputs and recurrent inputs) via two arguments on the recurrent layers, namely dropout for inputs and recurrent_dropout for recurrent inputs.
LSTM(32, dropout=0.5, recurrent_dropout=0.5)
Dense(1)
Dropout Regularization Binary Classification Example¶
In this section, we will demonstrate how to use dropout regularization to reduce overfitting using similar data from the previous example using just a fewer number of samples to encourage overfitting.
Overfit Multilayer Perceptron¶
The model will have one hidden layer with more nodes than may be required to solve this problem, providing an opportunity to overfit. We will also train the model for longer than is required to ensure the model overfits.
# generate 2d classification dataset
X, y = make_circles(n_samples=100, noise=0.1, random_state=1)
fig, ax = plt.subplots(figsize=(10,6))
# select indices of points with each class label
for i in range(2):
samples_ix = np.where(y == i)
plt.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i), s=50, alpha=0.5)
plt.legend()
plt.show()
# split into train and test
n_train = 30
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(500, input_dim=2, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=4000, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.legend()
plt.show()
We can see that expected shape of an overfit model where test accuracy increases to a point and then begins to decrease again.
Overfit MLP With Dropout Regularization¶
We can update the example to use dropout regularization. We can do this by simply inserting a new Dropout layer between the hidden layer and the output layer. In this case, we will specify a dropout rate (probability of setting outputs from the hidden layer to zero) to $40\%$ or $0.4$.
# define model
model = Sequential()
model.add(Dense(500, input_dim=2, activation='relu'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=4000, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.legend()
plt.show()
Model accuracy on both the train and test sets continues to increase to a plateau, albeit with a lot of noise given the use of dropout during training.
Extensions to explore.¶
- Input Dropout. Update the example to use dropout on the input variables and compare results.
- Weight Constraint. Update the example to add a max-norm weight constraint to the hidden layer and compare results.
- Repeated Evaluation. Update the example to repeat the evaluation of the overfit and dropout model and summarize and compare the average results.
- Grid Search Rate. Develop a grid search of dropout probabilities and report the relationship between dropout rate and test set accuracy.
Training Neural Networks With Noise¶
Training a neural network with a small dataset can cause the network to memorize all training examples, in turn leading to overfitting and poor performance on a holdout dataset.
Small datasets may also represent a harder mapping problem for neural networks to learn, given the patchy or sparse sampling of points in the high-dimensional input space.
Adding noise is one approach to making the input space smoother and easier to learn is to add noise to inputs during training.
Add Random Noise During Training¶
One approach to improving generalization error and to improving the structure of the mapping problem is to add random noise. At first, this sounds like a recipe for making learning more challenging. It is a counter-intuitive suggestion to improving performance because one would expect noise to degrade performance of the model during training.
The addition of noise during the training of a neural network model has a regularization effect and, in turn, improves the robustness of the model. It has been shown to have a similar impact on the loss function as the addition of a penalty term, as in the case of weight regularization methods.
In effect, adding noise expands the size of the training dataset. Each time a training sample is exposed to the model, random noise is added to the input variables making them different every time it is exposed to the model. In this way, adding noise to input samples is a simple form of data augmentation.
Adding noise means that the network is less able to memorize training samples because they are changing all of the time, resulting in smaller network weights and a more robust network that has lower generalization error.
How and Where to Add Noise¶
The most common type of noise used during training is the addition of Gaussian noise to input variables.
Gaussian noise, or white noise, has a mean of zero and a standard deviation of one and can be generated as needed using a pseudorandom number generator. The amount of noise added (eg. the spread or standard deviation) is a configurable hyperparameter. Too little noise has no effect, whereas too much noise makes the mapping function too challenging to learn.
The standard deviation of the random noise controls the amount of spread and can be adjusted based on the scale of each input variable. It can be easier to configure if the scale of the input variables has first been normalized.
Noise is only added during training. No noise is added during the evaluation of the model or when the model is used to make predictions on new data.
The addition of noise is also an important part of automatic feature learning, such as in the case of autoencoders, so-called denoising autoencoders that explicitly require models to learn robust features in the presence of noise added to inputs.
Although additional noise to the inputs is the most common and widely studied approach, random noise can be added to other parts of the network during training. Some examples include:
- Add noise to activations, i.e. the outputs of each layer.
- Add noise to weights, i.e. an alternative to the inputs.
- Add noise to the gradients, i.e. the direction to update weights.
- Add noise to the outputs, i.e. the labels or target variables.
The addition of noise to the layer activations allows noise to be used at any point in the network. This can be -beneficial for very deep networks. Noise can be added to the layer outputs themselves, but this is more likely achieved via the use of a noisy activation function.
The addition of noise to weights allows the approach to be used throughout the network in a consistent way instead of adding noise to inputs and layer activations. This is particularly useful in recurrent neural networks.
The addition of noise to gradients focuses more on improving the robustness of the optimization process itself rather than the structure of the input domain. The amount of noise can start high at the beginning of training and decrease over time, much like a decaying learning rate. This approach has proven to be an effective method for very deep networks and for a variety of different network types.
If the problem domain is believed or expected to have mislabeled examples, then the addition of noise to the class label can improve the model’s robustness to this type of error. Although, it can be easy to derail the learning process.
Adding noise to a continuous target variable in the case of regression or time series forecasting is much like the addition of noise to the input variables and may be a better use case.
Tips for Adding Noise During Training¶
Problem Types for Adding Noise¶
Noise can be added to training regardless of the type of problem that is being addressed.
It is appropriate to try adding noise to both classification and regression type problems.
The type of noise can be specialized to the types of data used as input to the model, for example, two-dimensional noise in the case of images and signal noise in the case of audio data.
Add Noise to Different Network Types¶
Adding noise during training is a generic method that can be used regardless of the type of neural network that is being used.
It was a method used primarily with multilayer Perceptrons given their prior dominance, but can be and is used with Convolutional and Recurrent Neural Networks.
Rescale Data First¶
It is important that the addition of noise has a consistent effect on the model.
This requires that the input data is rescaled so that all variables have the same scale, so that when noise is added to the inputs with a fixed variance, it has the same effect. The also applies to adding noise to weights and gradients as they too are affected by the scale of the inputs.
This can be achieved via standardization or normalization of input variables. If random noise is added after data scaling, then the variables may need to be rescaled again, perhaps per mini-batch.
Test the Amount of Noise¶
You cannot know how much noise will benefit your specific model on your training dataset.
Experiment with different amounts, and even different types of noise, in order to discover what works best. Be systematic and use controlled experiments, perhaps on smaller datasets across a range of values.
Noisy Training Only¶
Noise is only added during the training of your model.
Be sure that any source of noise is not added during the evaluation of your model, or when your model is used to make predictions on new data.
Noise Regularization in Keras¶
Keras supports the addition of noise to models via the GaussianNoise layer.
This is a layer that will add noise to inputs of a given shape. The noise has a mean of zero and requires that a standard deviation of the noise be specified as a parameter. For example
# import noise layer
from keras.layers import GaussianNoise
# define noise layer
layer = GaussianNoise(0.1)
The output of the layer will have the same shape as the input, with the only modification being the addition of noise to the values.
Noise Regularization in Models¶
The GaussianNoise can be used in a few different ways with a neural network model.
Firstly, it can be used as an input layer to add noise to input variables directly. This is the traditional use of noise as a regularization method in neural networks.
Below is an example of defining a GaussianNoise layer as an input layer for a model that takes $2$ input variables.
GaussianNoise(0.01, input_shape=(2,))
Noise can also be added between hidden layers in the model. Given the flexibility of Keras, the noise can be added before or after the use of the activation function. It may make more sense to add it before the activation; nevertheless, both options are possible.
Below is an example of a GaussianNoise layer that adds noise to the linear output of a Dense layer before a rectified linear activation function (ReLU), perhaps a more appropriate use of noise between hidden layers.
Dense(32)
GaussianNoise(0.1)
Activation('relu')
Dense(32)
Noise can also be added after the activation function, much like using a noisy activation function. One downside of this usage is that the resulting values may be out-of-range from what the activation function may normally provide. For example, a value with added noise may be less than zero, whereas the relu activation function will only ever output values $>= 0$.
Dense(32, activation='relu')
GaussianNoise(0.1)
Dense(32)
Noise Regularization Binary Classification Example¶
We will demonstrate how to use noise regularization to reduce overfitting using the same data in the previous example.
Overfit Multilayer Perceptron¶
We can develop an MLP model to address this binary classification problem.
The model will have one hidden layer with more nodes than may be required to solve this problem, providing an opportunity to overfit. We will also train the model for longer than is required to ensure the model overfits.
# define model
model = Sequential()
model.add(Dense(500, input_dim=2, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=4000, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.legend()
plt.show()
We can see that expected shape of an overfit model where test accuracy increases to a point and then begins to decrease again.
MLP With Input Layer Noise¶
The dataset is defined by points that have a controlled amount of statistical noise.
Nevertheless, because the dataset is small, we can add further noise to the input values. This will have the effect of creating more samples or resampling the domain, making the structure of the input space artificially smoother. This may make the problem easier to learn and improve generalization performance.
We can add a GaussianNoise layer as the input layer. The amount of noise must be small. Given that the input values are within the range $[0, 1]$, we will add Gaussian noise with a mean of $0.0$ and a standard deviation of $0.01$, chosen arbitrarily.
# define model
model = Sequential()
model.add(GaussianNoise(0.01, input_shape=(2,)))
model.add(Dense(500, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=4000, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.legend()
plt.show()
We clearly see the impact of the added noise on the evaluation of the model during training as graphed on the line plot. The noise causes the accuracy of the model to jump around during training, possibly due to the noise introducing points that conflict with true points from the training dataset.
Perhaps a lower input noise standard deviation would be more appropriate.
The model still shows a pattern of being overfit, with a rise and then fall in test accuracy over training epochs.
MLP With Hidden Layer Noise¶
An alternative approach to adding noise to the input values is to add noise between the hidden layers.
This can be done by adding noise to the linear output of the layer (weighted sum) before the activation function is applied, in this case a rectified linear activation function. We can also use a larger standard deviation for the noise as the model is less sensitive to noise at this level given the presumably larger weights from being overfit. We will use a standard deviation of $0.1$, again, chosen arbitrarily.
# define model
model = Sequential()
model.add(Dense(500, input_dim=2))
model.add(GaussianNoise(0.1))
model.add(Activation('relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=4000, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.legend()
plt.show()
In this case, we can see a marked increase in the performance of the model on the hold out test set.
We can also see from the line plot of accuracy over training epochs that the model no longer appears to show the properties of being overfit.
We can also experiment and add the noise after the outputs of the first hidden layer pass through the activation function.
# define model
model = Sequential()
model.add(Dense(500, input_dim=2, activation='relu'))
model.add(GaussianNoise(0.1))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=4000, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
# plot history
plt.plot(history.history['accuracy'], label=f'train, accuracy {round(train_acc, 3)}')
plt.plot(history.history['val_accuracy'], label=f'test, accuracy {round(test_acc, 3)}')
plt.legend()
plt.show()
Surprisingly, we see an increase in the performance of the model.
Again, we can see from the line plot of accuracy over training epochs that the model no longer shows sign of overfitting.
Extensions to explore.¶
- Repeated Evaluation. Update the example to use repeated evaluation of the model with and without noise and report performance as the mean and standard deviation over repeats.
- Grid Search Standard Deviation. Develop a grid search in order to discover the amount of noise that reliably results in the best performing model.
- Input and Hidden Noise. Update the example to introduce noise at both the input and hidden layers of the model.