Introduction to Predictive Analytics in Python¶
Predictive analytics encompasses a variety of statistical techniques from data mining, predictive modelling, and machine learning, that analyze current and historical facts to make predictions about future or otherwise unknown events.
In business, predictive models exploit patterns found in historical and transactional data to identify risks and opportunities. Models capture relationships among many factors to allow assessment of risk or potential associated with a particular set of conditions, guiding decision-making for candidate transactions.
The defining functional effect of these technical approaches is that predictive analytics provides a predictive score (probability) for each individual (customer, employee, healthcare patient, product SKU, vehicle, component, machine, or other organizational unit) in order to determine, inform, or influence organizational processes that pertain across large numbers of individuals.
Where Predictive analytics is used:
- marketing
- financial services
- insurance
- retail
- healthcare
- capacity planning
- and more...
import pandas as pd
import numpy as np
pd.set_option('display.max_columns', None)
fpath = 'https://assets.datacamp.com/production/repositories/1441/datasets/7abb677ec52631679b467c90f3b649eb4f8c00b2/basetable_ex2_4.csv'
df = pd.read_csv(fpath)
df.info()
df['id'] = np.arange(1,25001,1)
df['gender'] = np.where(df['gender_F'] == 1, 'F','M')
df.head()
basetable = df[['id', 'target', 'gender', 'age']]
basetable.head()
Visualize Target Distribution¶
import matplotlib.pyplot as plt
import seaborn as sns
total = len(df)
plt.figure(figsize=(7,5))
g = sns.countplot(x='target', data=df)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
height = p.get_height()
g.text(p.get_x()+p.get_width()/2.,
height + 1.5,
'{:1.2f}%'.format(height/total*100),
ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()
There is a severe class imbalance in the dataset
Visualize Data Correlation¶
plt.figure(figsize=(15, 8))
corr = df.drop(['id','gender'], axis=1).corr()
mask = np.tri(*corr.shape).T
sns.heatmap(corr.abs(), mask=mask, annot=True)
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show()
Visualize Data Correlation to Target¶
import matplotlib.cm as cm
n_fts = len(df.drop(['id','gender'], axis=1).columns)
colors = cm.rainbow(np.linspace(0, 1, n_fts))
_ = df.drop(['target', 'id','gender'], axis=1).corrwith(df.target).sort_values(ascending=True).plot(kind='barh',
color=colors, figsize=(10, 4))
plt.title('Correlation to Target')
plt.show()
Exploring the base table¶
Before diving into model building, it is important to understand the data you are working with. In this exercise, we will learn how to obtain the population size, number of targets and target incidence (target frequency) from a given basetable.
# Assign the number of rows in the basetable to the variable 'population_size'.
population_size = len(basetable)
# Print the population size.
print(f'population_size = {population_size}')
# Assign the number of targets to the variable 'targets_count'.
targets_count = sum(basetable['target'])
# Print the number of targets.
print(f'number of targets = {targets_count}')
# Print the target incidence.
print(f'target incidence: {targets_count / population_size}')
Exploring the predictive variables¶
It is always useful to get a better understanding of the population. Therefore, one can have a closer look at the predictive variables.
# Count and print the number of females.
print('number of females =', sum(basetable['gender'] == 'F'))
# Count and print the number of males.
print('number of males =', sum(basetable['gender'] == 'M'))
Logistic regression: the logit or sigmoid function¶

- Output of $a \ast x + b$ is a real number
- We want to predict a $0$ or a $1$
- Logit function transforms $a \ast x + b$ to a probability
Multivariate logistic regression¶
- Univariate: $ax + b$
- Multivariate: $a_1 x_1 + a_2 x_2 + \dots + a_n x_n + b$
Building a logistic regression model¶
# Import linear_model from sklearn.
from sklearn import linear_model
import warnings
warnings.filterwarnings('ignore')
# Create a dataframe X that only contains the candidate predictors age, gender_F and time_since_last_gift.
X = df[['age', 'gender_F', 'time_since_last_gift']]
# Create a dataframe y that contains the target.
y = df[['target']]
# Create a logistic regression model logreg and fit it to the data.
logreg = linear_model.LogisticRegression()
logreg.fit(X, y)
Showing the coefficients and intercept¶
Once the logistic regression model is ready, it can be interesting to have a look at the coefficients to check whether the model makes sense.
Given a fitted logistic regression model logreg, you can retrieve the coefficients using the attribute coef_. The order in which the coefficients appear, is the same as the order in which the variables were fed to the model. The intercept can be retrieved using the attribute intercept_.
# Construct a logistic regression model that predicts the target using age, gender_F and time_since_last gift
predictors = ["age","gender_F","time_since_last_gift"]
X = df[predictors]
y = df[["target"]]
logreg = linear_model.LogisticRegression()
logreg.fit(X, y)
# Assign the coefficients to a list coef
coef = logreg.coef_
for p,c in zip(predictors,list(coef[0])):
print(p + ' = ' + str(c))
# Assign the intercept to the variable intercept
intercept = logreg.intercept_
print('intercept = ', intercept[0])
Making predictions¶
Once your model is ready, you can use it to make predictions for a campaign. It is important to always use the latest information to make predictions.
In this exercise we will, given a fitted logistic regression model, learn how to make predictions for a new, updated basetable.
# Fit a logistic regression model
from sklearn import linear_model
X = df[:21500][["age","gender_F","time_since_last_gift"]]
y = df[:21500][["target"]]
logreg = linear_model.LogisticRegression()
logreg.fit(X, y)
# Create a dataframe new_data from current_data that has only the relevant predictors
new_data = df[21500:][["age","gender_F","time_since_last_gift"]]
# Make a prediction for each observation in new_data and assign it to predictions
predictions = logreg.predict_proba(new_data)
print(predictions[0:5])
Donor that is most likely to donate¶
The predictions that result from the predictive model reflect how likely it is that someone is a target. For instance, assume that you constructed a model to predict whether a donor will donate more than 50 Euro for a certain campaign. If the prediction for a certain donor is 0.82, it means that there is an 82% chance that he will donate more than 50 Euro.
In this exercise we will find the donor that is most likely to donate more than 50 Euro.
predictions = pd.DataFrame({'donor_ID': df[21500:].id,
'probability':predictions[:,1] })
# Sort the predictions
predictions_sorted = predictions.sort_values(['probability'])
# Print the row of predictions_sorted that has the donor that is most likely to donate
print(predictions_sorted.tail(1))
The donor that is most likely to donate still has a rather low probability to donate, this is due to the fact that the overall target incidence is low.
Variable selection¶
Drawbacks of models with many variables:
- Over-fitting
- Hard to maintain or implement
- Hard to interpret, multi-collinearity
Calculating AUC¶
The AUC value assesses how well a model can order observations from low probability to be target to high probability to be target. In Python, the roc_auc_score function can be used to calculate the AUC of the model. It takes the true values of the target and the predictions as arguments.
from sklearn.metrics import roc_auc_score
# Make predictions
predictions = logreg.predict_proba(X)
predictions_target = predictions[:,1]
# Calculate the AUC value
auc = roc_auc_score(y, predictions_target)
print(round(auc,2))
Using different sets of variables¶
Adding more variables and therefore more complexity to your logistic regression model does not automatically result in more accurate models. In this exercise we will verify whether adding 3 variables to a model leads to a more accurate model.
variables_1 = ['mean_gift', 'income_low']
variables_2 = ['mean_gift', 'income_low', 'gender_F', 'country_India', 'age']
# Create appropriate dataframes
X_1 = df[variables_1]
X_2 = df[variables_2]
y = df[["target"]]
# Create the logistic regression model
logreg = linear_model.LogisticRegression()
# Make predictions using the first set of variables and assign the AUC to auc_1
logreg.fit(X_1, y)
predictions_1 = logreg.predict_proba(X_1)[:,1]
auc_1 = roc_auc_score(y, predictions_1)
# Make predictions using the second set of variables and assign the AUC to auc_2
logreg.fit(X_2, y)
predictions_2 = logreg.predict_proba(X_2)[:,1]
auc_2 = roc_auc_score(y, predictions_2)
# Print auc_1 and auc_2
print(round(auc_1,2))
print(round(auc_2,2))
The model with $5$ variables has almost he same AUC as the model using only $2$ variables. Adding more variables doesn't always increase the AUC.
The forward stepwise variable selection procedure¶
- Empty set
- Find best variable $v_1$
- Find best variable $v_2$ in combination with $v_1$
- Find best variable $v_3$ in combination with $v_1 , v_2$
(Until all variables are added or until predefined number of variables is added)
Implementation of the forward stepwise procedure¶
- Function
aucthat calculates AUC given a certain set of variables - Function
best_nextthat returns next best variable in combination with current variables - Loop until desired number of variables is reached
Selecting the next best variable¶
The forward stepwise variable selection method starts with an empty variable set and proceeds in steps, where in each step the next best variable is added.
The auc function calculates for a given set of variables the AUC of the model that uses this variable set as predictors. The next_best function calculates which variable should be added in the next step to the variable list.
def auc(variables, target, df):
X = df[variables]
Y = df[target]
logreg = linear_model.LogisticRegression()
logreg.fit(X, Y)
predictions = logreg.predict_proba(X)[:,1]
auc = roc_auc_score(Y, predictions)
return(auc)
def next_best(current_variables, candidate_variables, target, df):
best_auc = -1
best_variable = None
# Calculate the auc score of adding v to the current variables
for v in candidate_variables:
auc_v = auc(current_variables + [v], target, df)
# Update best_auc and best_variable adding v led to a better auc score
if auc_v >= best_auc:
best_auc = auc_v
best_variable = v
return best_variable
# Calculate the AUC of a model that uses "max_gift", "mean_gift" and "min_gift" as predictors
auc_current = auc(['max_gift', 'mean_gift', 'min_gift'], ["target"], df)
print(round(auc_current,4))
# Calculate which variable among "age" and "gender_F" should be added to the variables "max_gift", "mean_gift" and "min_gift"
next_variable = next_best(['max_gift', 'mean_gift', 'min_gift'], ['age', 'gender_F'], ["target"], df)
print(next_variable)
The model that has age as next variable has a better AUC than the model that has gender_F as next variable. Therefore, age is selected as the next best variable.
# Calculate the AUC of a model that uses "max_gift", "mean_gift", "min_gift" and "age" as predictors
auc_current_age = auc(['max_gift', 'mean_gift', 'min_gift', 'age'], ["target"], df)
print(round(auc_current_age,4))
# Calculate the AUC of a model that uses "max_gift", "mean_gift", "min_gift" and "gender_F" as predictors
auc_current_gender_F = auc(['max_gift', 'mean_gift', 'min_gift','gender_F'], ["target"], df)
print(round(auc_current_gender_F,4))
Finding the order of variables¶
The forward stepwise variable selection procedure starts with an empty set of variables, and adds predictors one by one. In each step, the predictor that has the highest AUC in combination with the current variables is selected.
# Find the candidate variables
candidate_variables = list(df.drop(['target', 'id', 'gender'], axis=1).columns.values)
# Initialize the current variables
current_variables = []
# The forward stepwise variable selection procedure
number_iterations = 10
for i in range(0, number_iterations):
next_variable = next_best(current_variables, candidate_variables, ["target"], df)
current_variables = current_variables + [next_variable]
candidate_variables.remove(next_variable)
print("Variable added in step " + str(i+1) + " is " + next_variable + ".")
print('\n', current_variables)
# Create liist of all original predictor variables
og_list = list(df.drop(['target', 'id', 'gender'], axis=1).columns.values)
# Loop through all original predictor variables to find the unincluded variables from the selection procedure
for i in og_list:
if i not in current_variables:
print(i)
Correlated variables¶
The first $10$ variables that are added to the model are the following:
['max_gift', 'number_gift', 'time_since_last_gift', 'mean_gift', 'age', 'gender_F', 'country_India', 'income_high', 'min_gift', 'country_USA']
As you can see, time_since_first_gift is not added. Does this mean that it is a bad variable? You can test the performance of the variable by using it in a model as a single variable and calculating the AUC. How does the AUC of time_since_first_gift compare to the AUC of income_high? To this end, you can use the function auc()
It can happen that a good variable is not added because it is highly correlated with a variable that is already in the model. You can test this calculating the correlation between these variables
# Calculate the AUC of the model using time_since_first_gift only
auc_min_gift = auc(["time_since_first_gift"],["target"], df)
print(round(auc_min_gift,2))
# Calculate the AUC of the model using income_high only
auc_income_high = auc(["income_high"],["target"], df)
print(round(auc_income_high,2))
# Calculate the correlation between time_since_first_gift and time_since_last_gift
correlation = np.corrcoef(df["time_since_first_gift"], df["time_since_last_gift"])[0,1]
print(round(correlation,2))
Well done! You can observe that time_since_first_gift has more predictive power than income_high, but that it is has some positive correlation with time_since_last_gift and therefore not included in the selected variables.
Partitioning¶
In order to properly evaluate a model, one can partition the data in a train and test set. The train set contains the data the model is built on, and the test data is used to evaluate the model. This division is done randomly, but when the target incidence is low, it could be necessary to stratify, that is, to make sure that the train and test data contain an equal percentage of targets.
# Load the partitioning module
from sklearn.model_selection import train_test_split
# Create dataframes with variables and target
X = df.drop(['target', 'id', 'gender'], axis=1)
y = df["target"]
# Carry out 50-50 partititioning with stratification
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.50, stratify = y)
# Create the final train and test basetables
train = pd.concat([X_train, y_train], axis=1)
test = pd.concat([X_test, y_test], axis=1)
# Check whether train and test have same percentage targets
print(round(sum(train["target"])/len(train), 2))
print(round(sum(test["target"])/len(test), 2))
The stratify option makes sure the target incidence is the same in both train and test.
Evaluating a model on test and train¶
The function auc_train_test calculates the AUC of model that is built on a train set and evaluated on a test set
def auc_train_test(variables, target, train, test):
X_train = train[variables]
X_test = test[variables]
y_train = train[target]
y_test = test[target]
logreg = linear_model.LogisticRegression()
# Fit the model on train data
logreg.fit(X_train, y_train)
# Calculate the predictions both on train and test data
predictions_train = logreg.predict_proba(X_train)[:,1]
predictions_test = logreg.predict_proba(X_test)[:,1]
# Calculate the AUC both on train and test data
auc_train = roc_auc_score(y_train, predictions_train)
auc_test = roc_auc_score(y_test, predictions_test)
return(auc_train, auc_test)
# Apply the auc_train_test function
auc_train, auc_test = auc_train_test(["age", "gender_F", 'number_gift'], ["target"], train, test)
print(round(auc_train,2))
print(round(auc_test,2))
Building the AUC curves¶
The forward stepwise variable selection procedure provides an order in which variables are optimally added to the predictor set. In order to decide where to cut off the variables, you can make the train and test AUC curves. These curves plot the train and test AUC using the first, first two, first three, … variables in the model.
# Keep track of train and test AUC values
auc_values_train = []
auc_values_test = []
# Add variables one by one
variables_evaluate = []
# Iterate over the variables in current_variables the variables ordered according to the forward stepwise procedure
for v in current_variables:
# Add the variable
variables_evaluate.append(v)
# Calculate the train and test AUC of this set of variables
auc_train, auc_test = auc_train_test(variables_evaluate, ["target"], train, test)
# Append the values to the lists
auc_values_train.append(auc_train)
auc_values_test.append(auc_test)
res = pd.DataFrame(dict(variables=current_variables, auc=auc_values_test))
x = np.array(range(0,len(auc_values_train)))
y_train = np.array(auc_values_train)
y_test = np.array(auc_values_test)
plt.xticks(x, current_variables, rotation = 90)
plt.plot(x,y_train, label='Train')
plt.plot(x,y_test, label='Test')
plt.axvline(res.auc.idxmax(), linestyle='dashed', color='r', lw=1.5)
plt.ylim((0.6, 0.8))
plt.title(f'Best AUC = {round(res.auc.max(),3)}')
plt.legend()
plt.show()
best_vars = list(res[:res.auc.idxmax()+1].variables.values)
print(f'Best set of variables: \n{best_vars}')
Note that the test AUC curve starts declining sooner than the train curve. The point at which this happens is a good cut-off.
The cumulative gains curve¶
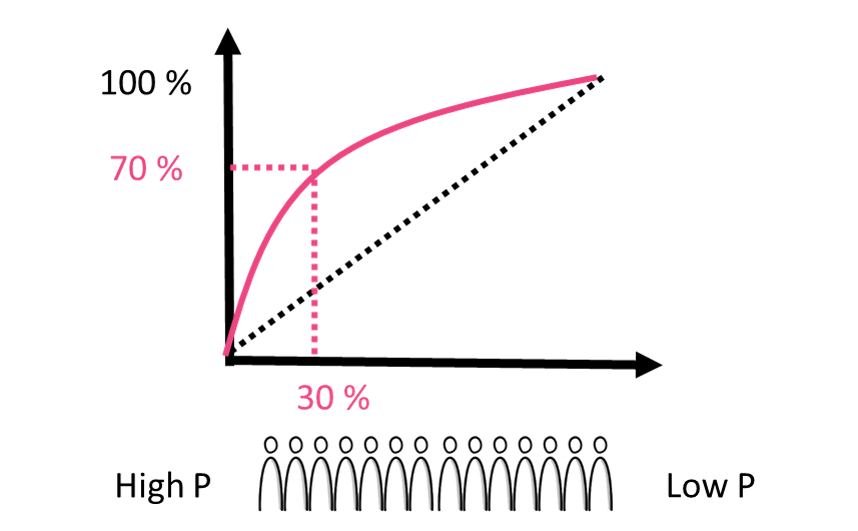
- Order all observations according to the output of the models probabilities
- On the left hand side are observations with the highest probability to be the targeted class according to the model, on the right hand side are the lowest probability observations.
- The X-axis is the percentage of observations being considered
- The y-axis is the percentage of the targeted class that is within the group on the X-axis
- Better models have higher cumulative gains
For the example above the cumulative gains is $70\%$ at $30\%$ meaning when taking the top $30\%$ of observations with the highest probability to be the targeted class, this group contains $70\%$ of the targeted class
Interpreting the cumulative gains curve¶
You built a model to predict which donors are most likely to react on a campaign and built a cumulative gains curve plotted below. Assume you have budget to send a letter to the top $30,000$ donors among the $100000$ donors. How many targets (donors that react) will you have reached, if there are $5000$ targets among the $100000$ donors?

- You have budget to reach $30\%$ of the donors. The cumulative gains graph shows that you reach $70\%$ of the $5000$ targets, which is $3500$ targets.
Constructing the cumulative gains curve¶
The cumulative gains curve is an evaluation curve that assesses the performance of your model. It shows the percentage of targets reached when considering a certain percentage of your population with the highest probability to be target according to your model.
# Fit the model on the best variables
X_train = train[best_vars]
X_test = test[best_vars]
y_train = train["target"]
y_test = test["target"]
logreg = linear_model.LogisticRegression()
# Fit the model on train data
logreg.fit(X_train, y_train)
# Calculate the predictions on the test data
predictions_test = logreg.predict_proba(X_test)
# Import the scikitplot module
import scikitplot as skplt
#Plot the cumulative gains graph
skplt.metrics.plot_cumulative_gain(y_test, predictions_test)
ax = plt.gca()
line = ax.lines[0]
xd = line.get_xdata()
yd = line.get_ydata()
plt.show()
A random model¶
In this exercise we will reconstruct the cumulative gains curve's baseline, that is, the cumulative gains curve of a random model.
import random
# Generate random predictions
random_predictions = [random.uniform(0,1) for _ in range(len(X_test))]
# Adjust random_predictions
random_predictions = [(r,1-r) for r in random_predictions]
# Plot the cumulative gains graph
skplt.metrics.plot_cumulative_gain(y_test, random_predictions)
plt.show()
You can observe that the cumulative gains curve of a random model aligns with the baseline.
The lift curve¶
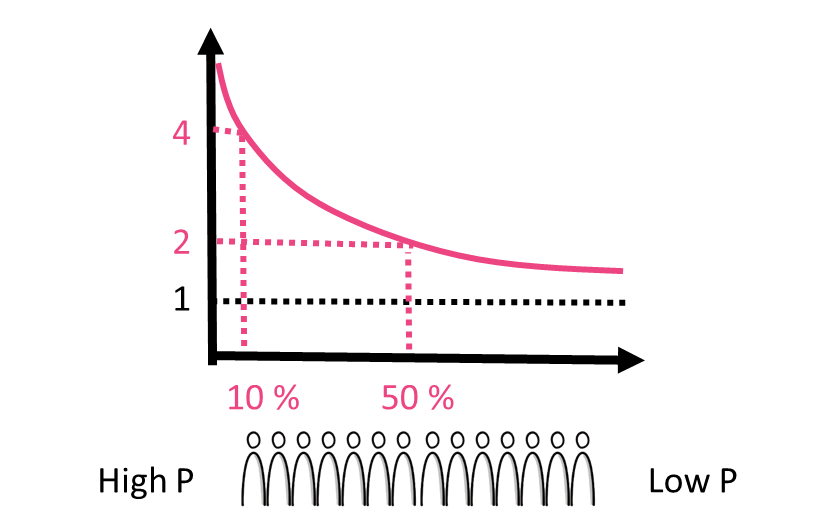
- The X-axis is the percentage of observations being considered ordered according to the output of the models probabilities
- The y-axis indicates how many times more than average the targeted class is included in the group on the X-axis
- Better models have higher lifts
In the first example above with the lift at $10\%$, and assume the top $10\%$ of observations contain $20\%$ of the target class. If the average percentage of the target class is $5\%$, the lift is $4$, because $20\%$ is $4$ times $5\%$
In the second example above with the lift at $50\%$, and assume the top $50\%$ of observations contain $10\%$ of the target class. If the average percentage of the target class is $5\%$, the lift is $2$, because $10\%$ is $2$ times $5\%$
Constructing the lift curve¶
The lift curve is an evaluation curve that assesses the performance of your model. It shows how many times more than average the model reaches targets.
# Plot the lift curve
skplt.metrics.plot_lift_curve(y_test, predictions_test)
plt.show()
A perfect model¶
In this exercise we will reconstruct the lift curve of a perfect model. To do so, we need to construct perfect predictions.
# Generate perfect predictions
perfect_predictions = [(1-target,target) for target in y_test]
# Plot the lift curve
skplt.metrics.plot_lift_curve(y_test, perfect_predictions)
plt.show()
You can observe that the lift is first $20$, which is normal as there are 5% targets: you can only have $20$ times more than average targets. After that the lift gradually decreases because there are no targets to add anymore.
Business case using lift curve¶
Here we will implement a function that calculates the profit of a campaign:
profit = profit(perc_targets, perc_selected, population_size, campaign_cost, campaign_reward)
In this method:
perc_targetsis the percentage of targets in the group that you select for your campaignperc_selectedthe percentage of people that is selected for the campaignpopulation_sizeis the total population sizecampaign_costis the cost of addressing a single person for the campaigncampaign_rewardis the reward of addressing a target
In this exercise we will learn for a specific case whether it is useful to use a model, by comparing the profit that is made when addressing all donors versus the top $40\%$ of the donors.
def profit(perc_targets, perc_selected, population_size, campaign_cost, campaign_reward):
cost = perc_selected * population_size * campaign_cost
reward = perc_targets * perc_selected * population_size * campaign_reward
profit = (reward - cost)
return profit
# Plot the lift graph
skplt.metrics.plot_lift_curve(y_test, predictions_test)
plt.show()
# Read the lift at 40% (round it up to the upper tenth)
perc_selected = 0.4
lift = 1.5
# Information about the campaign
population_size, target_incidence, campaign_cost, campaign_reward = 100000, 0.01, 1, 100
# Profit if all donors are targeted
profit_all = profit(target_incidence, 1, population_size, campaign_cost, campaign_reward)
print(f'profit_all = {round(profit_all, 2)}')
# Profit if top 40% of donors are targeted
profit_40 = profit(lift * target_incidence, 0.4, population_size, campaign_cost, campaign_reward)
print(f'\nprofit_40 = {round(profit_40, 2)}')
diff = abs(profit_all - profit_40)
print(f'\ndifference = {round(diff, 2)}')
When addressing the entire donor base, you do not make any profit at all. When using the predictive model, you can make $20,000$ Euro profit!
Business case using cumulative gains curve¶
The cumulative gains graph can be used to estimate how many donors one should address to make a certain profit. Indeed, the cumulative gains graph shows which percentage of all targets is reached when addressing a certain percentage of the population. If one knows the reward of a campaign, it follows easily how many donors should be targeted to reach a certain profit.
In this exercise, we will calculate how many donors we should address to obtain a $30,000$ Euro profit.
# Plot the cumulative gains
skplt.metrics.plot_cumulative_gain(y_test, predictions_test)
plt.show()
target_profit = 30000
camp_reward = 50
n_targets = 1000
pop_size = 10000
# Number of targets you want to reach
number_targets_toreach = target_profit / camp_reward
perc_targets_toreach = number_targets_toreach / n_targets
cumulative_gains = 0.4
number_donors_toreach = cumulative_gains * pop_size
print(f'Number of doners to reach = {number_donors_toreach}')
Predictor insight graphs¶
- Verify whether the variables in the model are interpretable
- Interpret the variables in the model and, verify whether the link between these variables and the target make sense
Retrieving information from the predictor insight table¶
The predictor insight graph table contains all the information needed to construct the predictor insight graph. For each value the predictor takes, it has the number of observations with this value and the target incidence within this group. The predictor insight graph table.
locals = ['USA', 'India', 'UK']
cnt_usa = df[df.country_USA == 1].country_USA.value_counts().values[0]
cnt_ind = df[df.country_India == 1].country_India.value_counts().values[0]
cnt_uk = df[df.country_UK == 1].country_UK.value_counts().values[0]
inc_usa = df[(df.country_USA == 1) & (df.target == 1)].country_USA.value_counts().values[0] / len(df.index)
inc_ind = df[(df.country_India == 1) & (df.target == 1)].country_India.value_counts().values[0] / len(df.index)
inc_uk = df[(df.country_UK == 1) & (df.target == 1)].country_UK.value_counts().values[0] / len(df.index)
pig_table = pd.DataFrame(dict(Country = locals, Size = [cnt_usa, cnt_ind, cnt_uk], Incidence = [inc_usa, inc_ind, inc_uk]))
pig_table
Discretization of a certain variable¶
In order to make predictor insight graphs for continuous variables, you first need to discretize them. In Python, you can discretize pandas columns using the qcut method.
# Discretize the variable time_since_last_donation in 10 bins
basetable = df.drop(['target', 'id', 'gender'], axis=1)
basetable["bins_recency"] = pd.qcut(basetable["time_since_last_gift"], 10)
# Print the group sizes
print(basetable.groupby("bins_recency").size())
Discretizing all variables¶
Instead of discretizing the continuous variables one by one, it is easier to discretize them automatically.
Only variables that are continuous should be discretized. You can verify whether variables should be discretized by checking whether they have more than a predefined number of different values.
basetable0 = df.drop(['id', 'gender'], axis=1)
# Print the columns in the original basetable
print(basetable0.columns)
# Get all the variable names except "target"
variables = list(basetable0.columns)
variables.remove("target")
# Loop through all the variables and discretize in 5 bins if there are more than 5 different values
for variable in variables:
if len(basetable0.groupby(variable)) > 5:
new_variable = "disc_" + variable
basetable0[new_variable] = pd.qcut(basetable0[variable], 5)
# Print the columns in the new basetable
print('\n', basetable0.columns)
Making clean cuts¶
The qcut method divides the variable in n_bins equal bins. In some cases, however, it is nice to choose your own bins. The method cut in python allows you to choose your own bins.
# Discretize the variable and assign it to basetable["disc_number_gift"]
basetable["disc_number_gift"] = pd.cut(basetable["number_gift"], [0,5,10,20])
# Count the number of observations per group
print(basetable.groupby("disc_number_gift").size())
Calculating average incidences¶
The most important column in the predictor insight graph table is the target incidence column. This column shows the average target value for each group.
# Select the income_high and target columns
basetable = df.drop(['id', 'gender'], axis=1)
basetable_income = basetable[["target","income_high"]]
# Group basetable_income by income_high
groups = basetable_income.groupby("income_high")
# Calculate the target incidence and print the result
incidence = groups["target"].agg(incidence = np.mean).reset_index()
#incidence.columns = ['income_high', 'incidence']
print(incidence)
You can observe that the higher a donor's income, the more likely he is to donate for the campaign.
Constructing the predictor insight graph table¶
In the previous exercise we learned how to calculate the incidence column of the predictor insight graph table. In this exercise, we will also add the size of the groups, and wrap everything in a function that returns the predictor insight graph table for a given variable.
# Function that creates predictor insight graph table
def create_pig_table(basetable, target, variable):
# Create groups for each variable
groups = basetable[[target,variable]].groupby(variable)
# Calculate size and target incidence for each group
pig_table = groups[target].agg(Incidence = np.mean, Size = np.size).reset_index()
# Return the predictor insight graph table
return pig_table
basetable = df.drop(['id', 'gender'], axis=1)
basetable['gender'] = np.where(basetable.gender_F == 1, 'Female', 'Male')
# Calculate the predictor insight graph table for the variable gender
pig_table_gender = create_pig_table(basetable, "target", "gender")
# Print the result
print(pig_table_gender)
The predictor insight graph table shows that females are more likely to donate than males.
Grouping all predictor insight graph tables¶
In the previous exercise, we constructed a function that calculates the predictor insight graph table for a given variable.
If you want to calculate the predictor insight graph table for many variables at once, it is a good idea to store them in a dictionary.
# Variables you want to make predictor insight graph tables for
variables = ["income_high", "gender_F", "disc_mean_gift", "disc_time_since_last_gift"]
# Create an empty dictionary
pig_tables = {}
# Loop through the variables
for variable in variables:
# Create a predictor insight graph table
pig_table = create_pig_table(basetable0, "target", variable)
# Add the table to the dictionary
pig_tables[variable] = pig_table
# Print the predictor insight graph table of the variable "disc_time_since_last_gift"
print(pig_tables["disc_time_since_last_gift"])
The predictor insight graph table shows that people who donated recently are more likely to donate again.
Plotting the incidences¶
The most important element of the predictor insight graph are the incidence values. For each group in the population with respect to a given variable, the incidence values reflect the percentage of targets in that group. In this exercise, we will write a python function that plots the incidence values of a variable, given the predictor insight graph table.
# The function to plot a predictor insight graph.
def plot_incidence(pig_table, variable):
# Plot the incidence line
pig_table["Incidence"].plot()
# Formatting the predictor insight graph
plt.xticks(np.arange(len(pig_table)), pig_table[variable])
plt.xlim([-0.5, len(pig_table) - 0.5])
plt.ylim([0, max(pig_table["Incidence"] * 2)])
plt.ylabel("Incidence", rotation=0, rotation_mode="anchor", ha="right")
plt.xlabel(variable)
# Show the graph
plt.show()
locals = df[['country_USA', 'country_India', 'country_UK']]
locals = locals.idxmax(1)
basetable0['country'] = locals
pig_table = create_pig_table(basetable0, "target", 'country')
plot_incidence(pig_table, "country")
Plotting the group sizes¶
The predictor insight graph gives information about predictive variables. Each variable divides the population in several groups. The predictor insight graph has a line that shows the average target incidence for each group, and a bar that shows the group sizes. In this exercise, we will write and apply a function that plots a predictor insight graph, given a predictor insight graph table.
# The function to plot a predictor insight graph
def plot_pig(pig_table, variable):
plt.figure(figsize=(10, 4))
# Plot formatting
plt.ylabel("Size", rotation=0, rotation_mode="anchor", ha="right")
# Plot the bars with sizes
pig_table["Size"].plot(kind="bar", width=0.5, color="lightgray", edgecolor="none")
# Plot the incidence line on secondary axis
pig_table["Incidence"].plot(secondary_y=True)
# Plot formatting
plt.xticks(np.arange(len(pig_table)), pig_table[variable])
plt.xlim([-0.5, len(pig_table) - 0.5])
plt.ylabel("Incidence", rotation=0, rotation_mode="anchor", ha="left")
plt.title(f'{variable}')
# Show the graph
plt.show()
# Apply the function for the variable "country"
plot_pig(pig_table, "country")
Putting it all together¶
Often, you want to make many predictor insight graphs at once. In this exercise, we will automatically do this using a for loop.
# Variables you want to make predictor insight graph tables for.
variables = ["income_high", "gender_F", "disc_mean_gift", "disc_time_since_last_gift"]
# Loop through the variables
for variable in variables:
# Create the predictor insight graph table
pig_table = create_pig_table(basetable0, "target", variable)
# Plot the predictor insight graph
plot_pig(pig_table, variable)