Logistic Regression¶
Logistic regression estimates a linear relationship between a set of features and a binary outcome (usually $1$ for yes and $0$ for no), mediated by a sigmoid function to ensure the model produces probabilities. The frequentist approach results in point estimates for the parameters that measure the influence of each feature on the probability that a data point belongs to the positive or negative class.
Logistic Function¶
The logistic function, also called the sigmoid function is an S-shaped curve that can take any real-valued number and map it into a value between $0$ and $1$ representing probability.
$$ f(x)={\frac {1}{1+e^{-k(x-x_{0})}}} $$where
- $x_{0} =$ the $x$ value of the sigmoid's midpoint,
- $k =$ the logistic growth rate or steepness of the curve,
- $e$ is the base of the natural logarithms or the
np.exp()function.
Representation Used for Logistic Regression¶
Logistic regression uses an equation as the representation, very much like linear regression.
Input values $(x)$ are combined linearly using weights or coefficient values (referred to as the Greek capital letter Beta $\beta$) to predict an output value $(y)$. A key difference from linear regression is that the output value being modeled is a binary values ($0$ or $1$) rather than a numeric value.
Example logistic regression equation:
$$y = \frac{e^{(\beta_0 + \beta_1*x)}}{(1 + e^{(\beta_0 + \beta_1*x)})}$$Where $y$ is the predicted output, $\beta_0$ is the bias or intercept term and $\beta_1$ is the coefficient for the single input value $(x)$. Each column in your input data has an associated $\beta$ coefficient (a constant real value) that must be learned from the training data.
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid", color_codes=True)
pd.set_option('display.max_columns', None)
Here we define a sigmoid function and plot it for a range of values between $-10$ and $10$
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-10,11,1)
y = sigmoid(x)
plt.plot(x,y)
plt.xlabel('X')
plt.ylabel('Sigmoid(X)');
Logistic Regression Example¶
Data Set¶
Quarterly US macro data from $1959 – 2009$
data = pd.DataFrame(sm.datasets.macrodata.load().data)
data.info()
data.head()
Data Prep¶
To obtain a binary target variable, we compute the $20$-quarter rolling average of the annual growth rate of quarterly real GDP. We then assign $1$ if current growth exceeds the moving average and $0$ otherwise. Finally, we shift the indicator variables to align next quarter's outcome with the current quarter.
data['growth_rate'] = data.realgdp.pct_change(4)
data['target'] = (data.growth_rate > data.growth_rate.rolling(20).mean()).astype(int).shift(-1)
data.quarter = data.quarter.astype(int)
data.tail()
pct_cols = ['realcons', 'realinv', 'realgovt', 'realdpi', 'm1', 'realgdp', 'pop', 'cpi', 'tbilrate', 'unemp']
drop_cols = ['year', 'growth_rate']
data.loc[:, pct_cols] = data.loc[:, pct_cols].pct_change(4)
data = pd.get_dummies(data.drop(drop_cols, axis=1), columns=['quarter']).dropna()
data.head()
data.info()
EDA¶
total = len(data)
plt.figure(figsize=(7,5))
g = sns.countplot(x='target', data=data)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
height = p.get_height()
g.text(p.get_x()+p.get_width()/2.,
height + 1.5,
'{:1.2f}%'.format(height/total*100),
ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()
plt.figure(figsize=(16, 8))
corr = data.corr()
mask = np.tri(*corr.shape).T
sns.heatmap(corr.abs(), mask=mask, annot=True, fmt=".3f", annot_kws={"size": 10})
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show()
import matplotlib.cm as cm
n_fts = len(data.drop('target', axis=1).columns)
colors = cm.rainbow(np.linspace(0, 1, n_fts))
_ = data.drop('target', axis=1).corrwith(data.target).sort_values(ascending=True).plot(kind='barh',
color=colors, figsize=(10, 4))
plt.title('Correlation to Target')
plt.show()
basetable0 = data.copy()
# Get all the variable names except "target"
variables = list(basetable0.columns)
variables.remove("target")
# Loop through all the variables and discretize in 5 bins if there are more than 5 different values
for variable in variables:
if len(basetable0.groupby(variable)) > 10:
new_variable = "disc_" + variable
basetable0[new_variable] = pd.qcut(basetable0[variable].round(4), 5)
# Print the columns in the new basetable
basetable0 = basetable0.drop(variables, axis=1)
print('\n', basetable0.columns)
# Function that creates predictor insight graph table
def create_pig_table(basetable, target, variable):
# Create groups for each variable
groups = basetable[[target,variable]].groupby(variable)
# Calculate size and target incidence for each group
pig_table = groups[target].agg(Incidence = np.mean, Size = np.size).reset_index()
# Return the predictor insight graph table
return pig_table
# Variables you want to make predictor insight graph tables for
variables = list(basetable0.columns)
variables.remove("target")
# Create an empty dictionary
pig_tables = {}
# Loop through the variables
for variable in variables:
# Create a predictor insight graph table
pig_table = create_pig_table(basetable0, "target", variable)
# Add the table to the dictionary
pig_tables[variable] = pig_table
# Print the predictor insight graph table of the variable "disc_realgdp"
print(pig_tables["disc_realgdp"])
# The function to plot a predictor insight graph
def plot_pig(pig_table, variable):
plt.figure(figsize=(10, 4))
# Plot formatting
plt.ylabel("Size", rotation=0, rotation_mode="anchor", ha="right")
# Plot the bars with sizes
pig_table["Size"].plot(kind="bar", width=0.5, color="pink", edgecolor="none", alpha=0.3)
# Plot the incidence line on secondary axis
pig_table["Incidence"].plot(secondary_y=True)
# Plot formatting
plt.xticks(np.arange(len(pig_table)), pig_table[variable])
plt.xlim([-0.5, len(pig_table) - 0.5])
plt.ylabel("Incidence", rotation=0, rotation_mode="anchor", ha="left")
plt.title(f'{variable}')
# Show the graph
plt.show()
# Loop through the variables
for variable in variables:
# Create the predictor insight graph table
pig_table = create_pig_table(basetable0, "target", variable)
# Plot the predictor insight graph
plot_pig(pig_table, variable)
Fit Logistic Regression¶
We use an intercept and convert the quarter values to dummy variables and train the logistic regression model as follows:
model = sm.Logit(data.target, sm.add_constant(data.drop('target', axis=1)))
result = model.fit()
result.summary()
This produces the following summary for our model with $198$ observations and $16$ variables, including intercept: The summary indicates that the model has been trained using maximum likelihood and provides the maximized value of the log-likelihood function at $-66.4$.
- likelihood function: The likelihood function (often simply called the likelihood) measures the goodness of fit of a statistical model to a sample of data for given values of the unknown parameters. It is formed from the joint probability distribution of the sample, but viewed and used as a function of the parameters only, thus treating the random variables as fixed at the observed values.
- The likelihood function represents the combination of model parameter values that maximize the probability of drawing the sample obtained.The procedure for obtaining these arguments of the maximum of the likelihood function is known as maximum likelihood estimation, which for computational convenience is usually done using the natural logarithm of the likelihood, known as the log-likelihood function.
- maximum likelihood estimation: Maximum likelihood estimation (MLE) is a method of estimating the parameters of a probability distribution by maximizing a likelihood function, so that under the assumed statistical model the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate.
# Image of model summary
plt.rc('figure', figsize=(12, 7))
plt.text(0.01, 0.05, str(result.summary()), {'fontsize': 14}, fontproperties = 'monospace')
plt.axis('off')
plt.tight_layout()
plt.subplots_adjust(left=0.2, right=0.8, top=0.8, bottom=0.1)
plt.savefig('logistic_example.png', bbox_inches='tight', dpi=300);
# Store p-values in dictionary
pvals = result.pvalues[1:].to_dict()
pvals
The LL-Null value of $-136.42$ is the result of the maximized log-likelihood function when only an intercept is included. It forms the basis for the pseudo-R2 statistic and the Log-Likelihood Ratio (LLR) test. The pseudo-R2 statistic is a substitute for the familiar R2 available under least squares. It is computed based on the ratio of the maximized log-likelihood function for the null model $m_0$ and the full model $m_1$.
The values vary from $0$ (when the model does not improve the likelihood) to 1 where the model fits perfectly and the log-likelihood is maximized at $0$. Consequently, higher values indicate a better fit.
Scikit Learn Example With Regularization¶
Regularization can be used to train models that generalize better on unseen data, by preventing the algorithm from overfitting the training dataset by penalizing the models coefficients.

Types of weight regularization:
- l1 (Lasso): Sum of the weights $$ \lambda \Sigma_{i=1}^{k} |w_{i}| $$
- l2 (Ridge): Sum of the square of weights $$ \lambda \Sigma_{i=1}^{k} w_{i}^{2} $$
- l1 + l2 (Elastic Net): Sum of the absolute and the squared weights.
Logistic regression with different types of regularization¶
Here, we fit a logistic regression model for the various types of regularization and without regularization. Then we evaluate with 3-fold cross validation.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score, StratifiedKFold, train_test_split, TimeSeriesSplit
from sklearn.metrics import roc_auc_score
#cv = StratifiedKFold(3)
cv = TimeSeriesSplit(n_splits=3)
X, y = data.drop('target', axis=1), data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, shuffle=False)
regs = ['l1', 'l2', 'none', 'elasticnet']
for reg in regs:
if reg == 'l1':
lr = LogisticRegression(penalty=reg, solver='liblinear', random_state=1)
print(f'{reg} cv score:', np.mean(cross_val_score(lr, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)))
elif reg == 'elasticnet':
lr = LogisticRegression(penalty=reg, solver='saga', l1_ratio=0.5, random_state=2)
print(f'\n{reg} cv score:', np.mean(cross_val_score(lr, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)))
else:
lr = LogisticRegression(penalty=reg, solver='lbfgs', random_state=3)
print(f'\n{reg} cv score:', np.mean(cross_val_score(lr, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)))
Logistic Regression Regularization Strength¶
To determine how strong we penalize our coefficients for logistic regression we adjust the $C$ parameter. The $C$ parameter is a penalty term used to disincentivise and regulate against over fitting.
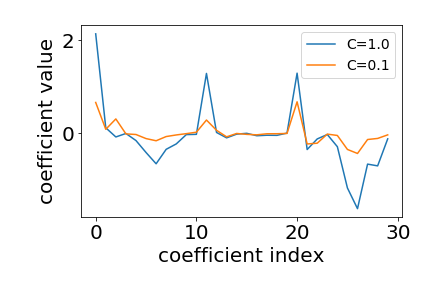
Here we evaluate $20$ parameter values for $C$ using cross validation. We then use the roc_auc_score to compare the predictive accuracy across the various regularization parameters as follows:
a = np.linspace(0, 1, 20)
b = [0.5]
Cs = np.sort(np.concatenate((a, b)))
enet_result, enet_coeffs = pd.DataFrame(), pd.DataFrame()
for i, C in enumerate(Cs):
print(C)
coeffs, test_results = [], []
lr_enet = LogisticRegression(penalty='elasticnet', solver='saga', l1_ratio=C, random_state=22, n_jobs=-1)
for train, test in cv.split(X.values, y.values):
X_train0 = X.iloc[train]
y_train0 = y.iloc[train]
lr_enet.fit(X_train0, y_train0)
coeffs.append(np.squeeze(lr_enet.coef_))
X_test0 = X.iloc[test]
y_test0 = y.iloc[test]
y_prob0 = lr_enet.predict_proba(X_test0)[:,1]
auc = roc_auc_score(y_test0, y_prob0)
test_results.append([auc, C])
test_results = pd.DataFrame(test_results, columns=['auc', 'C'])
enet_result = enet_result.append(test_results)
enet_coeffs[C] = np.mean(coeffs, axis=0)
enet_result.describe()
We can again plot the accuracy result for the range of hyperparameter values alongside the coefficient path that shows the improvements in predictive accuracy as the coefficients are a bit shrunk at the optimal regularization value $10^4$:
fig, axes = plt.subplots(ncols=2, sharex=True, figsize=(12,6))
best_C = enet_result.groupby('C').auc.mean().idxmax()
best_accuracy = enet_result.groupby('C').auc.mean().max()
mean_auc = enet_result.groupby('C').auc.mean().median()
enet_result.groupby('C')['auc'].mean().plot(logx=True, title='AUC Scores', ax=axes[0],
label=f'Best AUC = {round(best_accuracy,3)}')
axes[0].axhline(mean_auc, color='r', label=f'Mean AUC = {mean_auc}', ls='--')
axes[0].axvline(x=best_C, c='darkgrey', ls='--', label=f'Best C = {best_C}')
axes[0].set_xlabel('Regularization')
axes[0].set_ylabel('AUC')
axes[0].legend(loc='best')
enet_coeffs.T.plot(legend=False, logx=True, title='Elasticnet Path', ax=axes[1])
axes[1].set_xlabel('Regularization')
axes[1].set_ylabel('Coefficients')
axes[1].axvline(x=best_C, c='darkgrey', ls='--')
fig.tight_layout();
Feature Selection¶
The forward stepwise variable selection procedure¶
- Empty set
- Find best variable $v_1$
- Find best variable $v_2$ in combination with $v_1$
- Find best variable $v_3$ in combination with $v_1 , v_2$
(Until all variables are added or until predefined number of variables is added)
Implementation of the forward stepwise procedure¶
- Function
aucthat calculates AUC given a certain set of variables - Function
next_bestthat returns next best variable in combination with current variables - Loop until desired number of variables is reached
def auc(variables, target, df, multiple=True):
if multiple:
X0 = X[variables]
y0 = y
else:
X0 = X[[variables]]
y0 = y
logreg = LogisticRegression(penalty='elasticnet', solver='saga', l1_ratio=best_C,
random_state=22, n_jobs=-1)
score = np.mean(cross_val_score(logreg, X0, y0, scoring='roc_auc', cv=cv, n_jobs=-1))
return(score)
def next_best(current_variables, candidate_variables, target, df):
best_auc = -1
best_variable = None
# Calculate the auc score of adding v to the current variables
for v in candidate_variables:
auc_v = auc(current_variables + [v], target, df, multiple=True)
# Update best_auc and best_variable adding v led to a better auc score
if auc_v >= best_auc:
best_auc = auc_v
best_variable = v
return best_variable
Finding the order of variables¶
The forward stepwise variable selection procedure starts with an empty set of variables, and adds predictors one by one. In each step, the predictor that has the highest AUC in combination with the current variables is selected.
# Find the candidate variables
candidate_variables = list(data.drop('target', axis=1).columns.values)
# Initialize the current variables
current_variables = []
# The forward stepwise variable selection procedure
number_iterations = 16
for i in range(0, number_iterations):
next_variable = next_best(current_variables, candidate_variables, ["target"], data)
current_variables = current_variables + [next_variable]
candidate_variables.remove(next_variable)
print("Variable added in step " + str(i+1) + " is " + next_variable + ".")
print('\n', current_variables)
Evaluating a model with 3 fold-cv¶
# Keep track of AUC values
auc_values_cv = []
# Add variables one by one
variables_evaluate = []
# Iterate over the variables in current_variables the variables ordered according to the forward stepwise procedure
for v in current_variables:
# Add the variable
variables_evaluate.append(v)
# Calculate the AUC of this set of variables
auc_test = auc(variables_evaluate, 'target', data, multiple=True)
# Append the values to the lists
auc_values_cv.append(auc_test)
Finding the optimal set of features¶
The forward stepwise variable selection procedure provides an order in which variables are optimally added to the predictor set. In order to decide where to cut off the variables, we make the 3 fold-cv AUC curves. These curves plot the AUC using the first, first two, first three, … variables in the model.
res = pd.DataFrame(dict(variables=current_variables, auc=auc_values_cv))
x = np.array(range(0,len(auc_values_cv)))
y_cv = np.array(auc_values_cv)
plt.xticks(x, current_variables, rotation = 90)
plt.plot(x,y_cv, label='3-fold CV')
plt.axvline(res.auc.idxmax(), linestyle='dashed', color='r', lw=1.5)
plt.ylim((0.71, 0.99))
plt.title(f'Best AUC = {round(res.auc.max(),3)}')
plt.legend()
plt.show()
best_vars = list(res[:res.auc.idxmax()+1].variables.values)
print(f'Best set of variables: \n{best_vars}')
Explore logistic regression coefficients¶
The coefficients can be interpreted as the change in log odds of the target variable associated with $1$ unit increase in the the input feature value.
For example:
If the input feature is realinv in quarters then, an increase in realinv by one quarter will have an effect equal to the coefficient or the log odds.
The exponent of the coefficients will give us the change in the actual odds $O$ associated with a $1$ unit increase in the feature value
Odds: The probability of an even $p$ occurring divided by the probability of the event $p$ not occurring $ \frac{p}{1-p}$
We can go backwards to get the probability $p$ by calculating $p = \frac{O}{1+O}$
Note that:
- Probability ranges from $0$ to $1$
- Odds ratio range from $0$ to $\infty$
- Log Odds range from $-\infty$ to $\infty$
That is why the log odds are used to avoid modeling a variable with a restricted range such as probability.
We will now explore the coefficients of the logistic regression to understand what is driving our target variable to go up or down. Wee will extract the logistic regression coefficients from our fitted model, and calculate their exponent to make them more interpretable.
logreg = LogisticRegression(penalty='elasticnet', solver='saga', l1_ratio=best_C,
random_state=22, n_jobs=-1)
logreg.fit(X_train[best_vars], y_train)
# Combine feature names and coefficients into pandas DataFrame
feature_names = pd.DataFrame(X[best_vars].columns, columns=['Feature'])
log_coef = pd.DataFrame(np.transpose(logreg.coef_), columns=['Coefficient'])
coefficients = pd.concat([feature_names, log_coef], axis = 1)
coefficients['P-value'] = coefficients.Feature.map(pvals).values
# Calculate exponent of the logistic regression coefficients
coefficients['Odds_ratio'] = np.exp(coefficients['Coefficient']).round(3)
# Calculate the probability for each coefficient
coefficients['Probability'] = coefficients['Odds_ratio'] / (1 + coefficients['Odds_ratio'])
coefficients['Pct_odds_increase'] = (coefficients['Odds_ratio'] - 1) * 100
# Remove coefficients that are equal to zero
coefficients = coefficients[coefficients['Coefficient']!=0]
# Print the values sorted by the exponent coefficient
pd.set_option('display.float_format', lambda x: '%.3f' % x)
coefficients = coefficients.sort_values(by=['Odds_ratio'], ascending=False)
coefficients
# Filter only statistically significant coefficients
mask = coefficients['P-value'] <= 0.05
coefficients[mask]
Values $< 1$ decrease the odds values $> 1$ increase the odds
The coefficient for
realinv= $3.657$ which is interpreted as the expected change in log odds for a one-quarter increase in therealinv.The odds ratio can be calculated by exponentiating this value to get $38.756$ which means we expect to see about a $3,776\%$ increase in the odds of the quarterly real GDP growth exceeding its $20$-quarter rolling average, for a one-quarter increase in
realinv
Plot Receiver Operating Characteristic (ROC) with cross validation¶
from sklearn.metrics import auc
from sklearn.metrics import plot_roc_curve
vars_ = list(coefficients[mask].Feature.values)
n_samples, n_features = X[vars_].shape
classifier = LogisticRegression(penalty='l2', solver='lbfgs', C=best_C, n_jobs=-1, random_state=122)
X0, y0 = X[vars_].values, y.values
tprs = []
aucs = []
mean_fpr = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(12, 7))
for i, (train, test) in enumerate(cv.split(X0, y0)):
classifier.fit(X0[train], y0[train])
viz = plot_roc_curve(classifier, X0[test], y0[test],
name='ROC fold {}'.format(i),
alpha=0.5, lw=1, ax=ax)
interp_tpr = np.interp(mean_fpr, viz.fpr, viz.tpr)
interp_tpr[0] = 0.0
tprs.append(interp_tpr)
aucs.append(viz.roc_auc)
ax.plot([0, 1], [0, 1], linestyle='--', lw=1.5, color='k',
label='Chance', alpha=.8)
mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(aucs)
ax.plot(mean_fpr, mean_tpr, color='red', label=r'Mean ROC (AUC = %0.2f $\pm$ %0.2f)' % (mean_auc, std_auc), lw=1.5)
std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
ax.fill_between(mean_fpr, tprs_lower, tprs_upper, color='white', label=r'$\pm$ 1 std. dev.')
ax.set(xlim=[-0.05, 1.05], ylim=[-0.05, 1.05], title="Receiver operating characteristic")
ax.legend(loc="lower right")
plt.show()